Listen to Dance由音乐自动排舞
Dance motion generation是近年来兴起的研究,由音乐去自动生成排舞动作,是Dance motion generation的进一步发展和应用。Listen to Dance出自首尔大学的Music & Audio Research Group,实现了音乐到编舞的生成。专业舞蹈者在长期舞蹈创作中学习到了音乐和舞姿之间的联系和搭配,可以说是一种视觉和听觉建立的深层次的联系,这种关联在大数据支持下计算机是有理由去实现的。
论文引入
编舞是一种设计一系列动作的艺术,在表演艺术中,编舞延伸到使用人体来表达运动,并且这些通常用音乐来执行。适合音乐的编舞具有重要意义,因为它不仅是艺术品本身,而且最大化音乐的表达。因此,编舞已成为近年来许多流行音乐作品的基本要素。同时创建音乐编排的过程也被认为是重要的,并且正在积极地进行对能够自动生成编排的系统的研究。然而,自动编排生成是一项具有挑战性的任务,因为音乐和舞蹈都是抽象艺术概念,两个概念之间的明确关系也不是由既定规则定义的。
机器学习和深度学习技术的最新进展促进了研究舞蹈和音乐之间的关系的各种尝试。编排生成算法[1]通过检索与给定新音乐片段的预定动作音乐配对数据库中的最相似音乐片段相对应的动作作为编舞姿势。该方法从预定义的数据库中选择舞蹈动作,因此保证了与音乐高度相关的检索。然而,它具有局限性,因为它不能创造未包括在数据库中的新颖的舞蹈动作。基于Mel-Frequency倒谱系数(MFCC)特征对音乐类型进行分类,并根据结果生成匹配的编排[2]。但由于编排是通过类型分类器获得的分类值来确定的,因此生成新颖的编排是有限的。音乐驱动编排模型[3]使用成对的音乐和三维运动数据来训练Factored Conditional Restricted Boltzmann Machines(FCRBM),试图通过在训练过程中使用mel谱图来直接训练音乐和舞蹈之间的关系,但是编排的舞蹈不是特别流畅。
总的来说,在已有的研究中,编排生成算法和匹配编排不能够创造新颖的编排;音乐驱动编排模型确实成功创造了新颖的舞蹈动作,但未能取得好成绩,主要是因为训练数据仅有23分钟。Listen to Dance则是一种新颖的方法,总结一下它的优势:
- Listen to Dance一种基于神经网络的模型
- 从大量数据中进行训练,并且训练数据获取较为容易
- 该模型可以生成新的自然编排
实现模型
我们先来看一下模型实现结构:
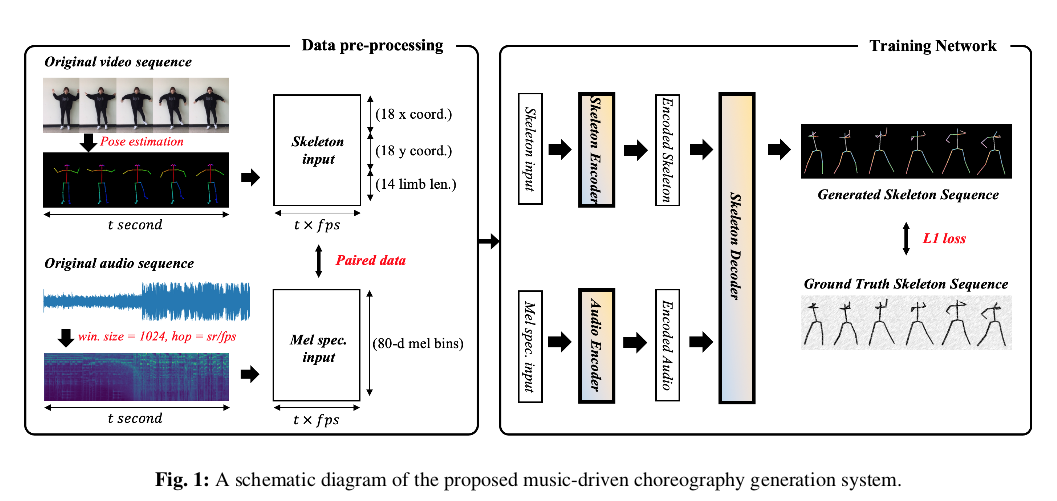
我们先总体分析一下网络结构,对于输入的舞蹈视频首先转换为骨架描述的人体结构视频,对于输入的对应音转换为声谱图,数据预处理后送入Encoder-Decoder网络,重构出骨架序列视频和真实进行损失优化。测试时,输入音频则可实现对应骨架序列视频(编舞)的生成。接下来,我们对这个过程展开分析。
数据预处理
对于输入的视频帧先要转换为对应的骨架帧,文章采用Openpose算法[4]实现,Openpose算法现在已经算是广发应用在人体姿态检测中,影响力还是很大的。提取每帧15个人体关节的x,y坐标,利用min-max标准化每个视频的提取坐标值,并对未识别的坐标值使用线性插值。由于无法使用2d关节坐标测量人体肢体之间的精确三维角度,因此文章使用每个点的绝对坐标值作为训练目标。另外计算了14个主要肢体的长度,并增加了与模型生成的骨骼的肢体长度进行比较的损失。因此,总共15个关节的x,y坐标和总共14个主肢长度被用作骨架数据,整体操作可以参考下图。
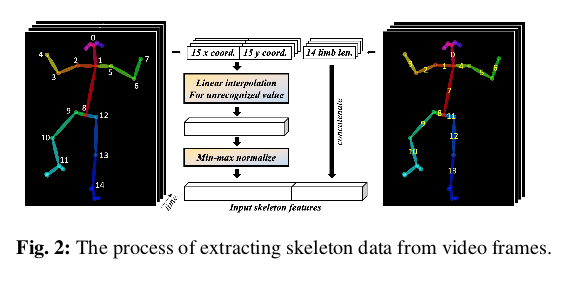
对于输入的音频,主要进行的是将声音信号转换为声谱图图像,时间轴为t秒(与骨架视频对应)。
CDHC Block
为了学习两种不同模态(即音乐和舞蹈)的时间序列数据之间的关系,需要一个执行多模态序列到序列变换的模型。文章修改了Dilated Convolution Text-To-Speech模型[5],该模型在text-tospeech域中表现良好,并将其用作模型的编排生成网络。文章使用的卷积网络为causal dilated highway convlutional block(CDHC),Causal意味着在计算时间$t$的输出时,只能参考从时间0到$t-1$的输入数据,网络必须是一个自动回归模型,以生成前一帧尚不知道的下一帧。Dilated Convolution称为空洞卷积,主要是为了增大编码的感受野,在WaveNet中也被使用。所谓的Highway就是出自Highway networks一文[6],它主要可以解决深层神经网络训练的困难的问题。
Encoder & Decoder
骨架编码器和音频编码器都包含三个卷积层和10个CDHC块。每个编码器的第一个卷积层将输入通道增加到256维,而另外两个层执行1x1卷积。此后,来自最后卷积层的输出值依次连接到10个CDHC块,扩张系数为(1,3,9,27,1,3,9,27,3,3),相应的操作促使音频和骨架数据被编码到感受野很广的特征空间,以反映足够的过去信息。解码器的输入是编码的骨架和编码的音频的融合,以此生成下一帧的骨架数据帧。首先,输入到解码器的编码骨架与编码音频组合如下:
\[\begin{equation} \begin{aligned} &H1 = conv(E_{skeleton}+E_{audio}[:128]) \\ &H2 = conv(E_{skeleton}+E_{audio}[128:]) \\ &comb = \sigma(H1) \cdot tanh(H2) \end{aligned} \end{equation}\]其中$E_{skeleton}$和$E_{audio}$分别表示编码骨架和编码音频,而conv表示卷积层,输出通道为128,内核大小为1。组合的张量然后通过六个CDHC块,扩张系数为(1,3,9,27,3,3),再通过三个具有tanh激活功能的128通道卷积层。最后,在通过具有与目标尺寸相同的输出通道的卷积层之后,通过sigmoid获得最终的解码器输出。
该网络从时间0到$t-1$接收骨架和音乐数据作为输入。两个数据都通过编码器编码,并在解码器的开头组合。解码器的最终输出在时间1到$t$与真实骨架数据进行比较,我们将其用作$L1$损耗。由于网络中包含的所有卷积运算都具有内核大小1或Causal操作,因此输出的第$k$个值仅来自0到$k-1$时间。因此,该模型满足自回归条件。这也为单独由音频生成骨架视频提供支持。
测试时,每个关节的初始位置被给出作为输入骨架框架,结合音频编码器得到$t=1$的骨架图,再送入编码,进而得到后续帧的骨架帧输出。
实验
论文让人去对生成的编舞和真实的以及随意产生的编舞进行打分,打分针对两个问题(Q1:编排是否自然?/ Q2:编排是否适合音乐?)结果如下:
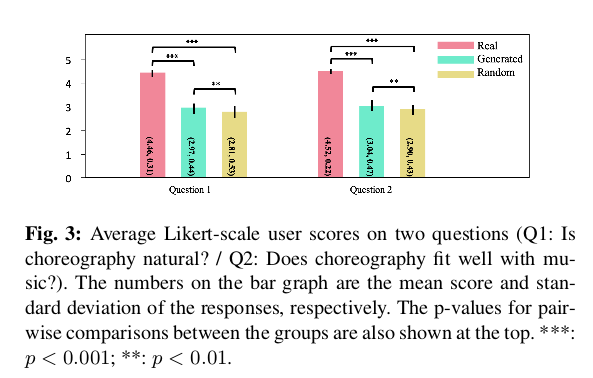
这两个问题的平均用户得分在Real组中最高,在Random组中最低,而生成的在中间,判断所提出的模型产生了适合音乐的编排。文章进一步对自相关进行了分析,以进一步研究生成的编排与实际编排之间的差异。自相关是给定序列与其自身之间的相关性,反映了序列的周期性特征。可以通过在自相关结果中观察到的峰的位置来识别给定序列的周期性分量。使用这个,通过计算编排运动的x,y坐标上的自相关来分析运动,并将其与相应音乐的速度进行比较。文章假设是,如果模型可以通过听音乐产生舞蹈,则运动的自相关峰值位置将出现在与音乐节拍相同的点上。
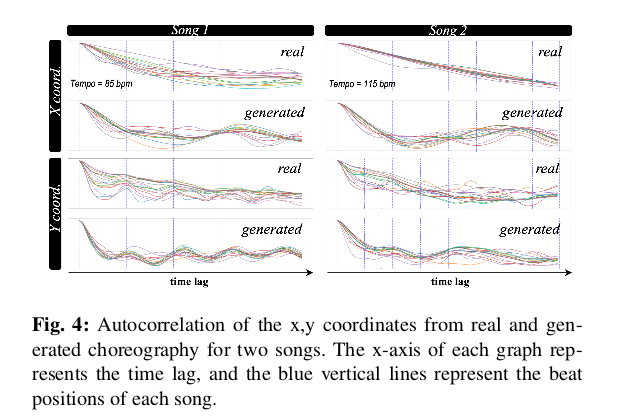
真实编舞中在y方向运动中观察到清晰的峰值,但在x方向运动中没有观察到。在生成的编排中也观察到这种趋势,判断出所提出的模型已经产生了听音乐并反映其周期性的编排。
总结
文章提出了一种自动回归编码器 - 解码器网络,可以为给定的音乐输入生成匹配的编排。文章使用从YouTube获取的音频 - 视频对数据进行训练。结果发现通过用户研究和自相关分析的比较产生了与音乐匹配的编舞。这是个有趣的应用,因为它在基于学习的编排生成领域表现出了显着的表现,一旦编舞性能上进一步提升的话完全可以取代舞者繁琐的编舞工作。
参考文献
[1] Minho Lee, Kyogu Lee, and Jaeheung Park, “Music similarity-based approach to generating dance motion sequence,” Multimedia tools and applications, vol. 62,no. 3, pp. 895–912, 2013.
[2] Ferda Ofli, Yasemin Demir, Yücel Yemez, Engin Erzin,A Murat Tekalp, Koray Balcı, İdil Kızoğlu, Lale Akarun, Cristian Canton-Ferrer, Joëlle Tilmanne, et al.,“An audio-driven dancing avatar,” Journal on Multimodal User Interfaces, vol. 2, no. 2, pp. 93–103, 2008.
[3] Omid Alemi, Jules Françoise, and Philippe Pasquier,“Groovenet: Real-time music-driven dance movement generation using artificial neural networks,” networks,vol. 8, no. 17, pp. 26, 2017.
[4] Zhe Cao, Tomas Simon, Shih-En Wei, and Yaser Sheikh,“Realtime multi-person 2d pose estimation using part affinity fields,” in CVPR, 2017.
[5] Hideyuki Tachibana, Katsuya Uenoyama, and Shunsuke Aihara, “Efficiently trainable text-to-speech system based on deep convolutional networks with guided attention,” arXiv preprint arXiv:1710.08969, 2017.
[6] Rupesh Kumar Srivastava, Klaus Greff, and Jürgen Schmidhuber, “Highway networks,” arXiv preprint arXiv:1505.00387, 2015.










