Localized GAN论文解读
GAN实现数据的从无到有是通过随机噪声z作为输入,在生成对抗下实现逼真数据的生成。这个过程是从全局的角度上直接生成数据样本, 很难分析具体的z对生成带来的影响。我们只知道在随机噪声z的作用下生成的数据样本和真实数据样本在分布上是随着网络的优化而逐渐相近的。为了进一步刻画数据的几何特性和数据样本的流形。 由齐国君团队在2018 CVPR上发表的Localized GAN通过局部坐标系来参数化不同位置的数据变换的局部几何, 缓解了GAN生成多样性不足的同时,还实现了在半监督分类的优化。
论文引入
经典的GAN试图生成与真实数据无法区分的样本。为此,它将生成器$G(z)$学习为从分布$P_z$的输入随机噪声$z$映射到输出数据$G(z)$的函数。 优化判别器以区分实际和生成的样本,生成器和鉴别器以对抗方式联合训练,达到生成器通过提高生成数据的质量来欺骗判别器。生成器生成的所有样本形成流形 $\mathcal M = \lbrace G(z) \vert z \sim P_z \rbrace$,这里的输入$z$为全局坐标。然而,全局坐标$z$可能无法捕获多种形式的局部变换。例如,就人脸而言, 人脸的高维数据在流形分析上可能在低维就可以表示,然而人脸的有无眼镜、胡须、帽子等,往往是在人脸流形上的细微变化影响的。
只有一个$z$变量去参数化整个流形,这个在流形学上是不现实的。在数学上,这种整体的参数化往往是不存在的,比如我们无法用一个参数坐标去覆盖整个球面。 这时需要借助于通过若干个局部的坐标系去覆盖整个流形。即便存在全局坐标$z$,但是对于全局GAN而言,还要面对几个无法避免的问题。首先,对于数据$x$, 如何确定$G(z) = x$呢?这个在传统GAN中是无法实现的,因为需要引入$G^{-1}$,这里可能要借助编码器进一步实现$z$的分析。再者,对于流形的切向量$\mathcal T_x$, 一旦切向量存在线性相关时,就有可能造成流形的一些折叠,即使$z$在不同方向上变化,$G(z)$也不会产生显着的数据变化。这就是所谓的GAN生成上的多样性不足问题, 这里文章利用几何角度去分析。
通过若干个局部的坐标系去覆盖整个流形是刻画数据流形的重要一步,如果在GAN的实现上利用局部坐标系$z$代替传统GAN下全局坐标$z$,是不是可以对数据的局部几何做更好的描述呢? 这个答案是肯定的,试想数据中的每一个样本点$x$都对应着局部坐标$z$或者是其附近的值,这样根据局部生成器$G(x,z)$可以实现数据更好地刻画和生成。 当局部坐标系足够的多,可以实现对全局流形的无缝描述,这也是Localized GAN的意义所在。
总结一下Localized GAN的优势:
- 通过局部坐标$z$可以实现数据的几何特性探索
- 论文在局部切线上施加正交性,缓解了生成多样性不足问题
- 给定一个图像x,用局部表示G(x,z)可以对这个x在它的局部领域中做各种编辑操作或者控制图像的各种属性
- 可以实现半监督分类任务的优化
Localized GAN实现
Localized GAN创建的局部坐标系是实现算法的关键,如何去构造这个局部坐标系呢?我们通过图例分析:
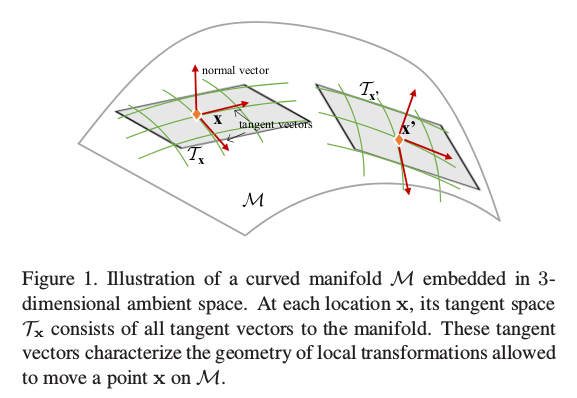
上图显示了在流形$\mathcal M$下,切空间$\mathcal T_x$包含了局部所有的切向量,这些切向量允许在$\mathcal M$上移动点$x$的局部变换的几何形状。 这将在x周围形成一个局部坐标图${ G(x,z) \vert z \subset \mathbb R^N \sim P_z }$,其局部坐标$z$从随机分布$P_z$绘制在欧几里德空间$\mathbb R^N$上。 以这种方式,局部坐标图集可以通过位于$\mathcal M$不同点处的局部生成器的集合覆盖整个流形$\mathcal M$。
为了研究点$x$附近的局部几何,需要位于流形上的$x$处的切向量。通过改变坐标$z^j$的值来修改其他坐标值,$G(x,z)$生成的点形成一个通过流形上$x$的坐标曲线。 然后,在$x$该坐标曲线的矢量正切为所有这样的N个切线矢量$\tau_x^j = 1,…,N$形成跨越$x$处的线性切线空间$\mathcal T_x = Span(\tau_x^1,…,\tau_x^N)$的基础。 这个切线空间由所有向量在流形上通过$x$的某些曲线的切线组成。每个切线$\tau \in \mathcal T_x$表征在该切线向量的方向上的一些局部变换。
流形$\mathcal M$的切向量如何表示呢?自然可以用偏导去实现,其中流形$\mathcal M$在局部坐标系$z$的偏导:
\[\begin{equation} \tau_x^j \triangleq \frac{\partial G(x,z)}{\partial z^j} \vert_{z=0} \in \mathbb R^D \end{equation}\]雅可比矩阵$J_x \in R^{D×N}$可以通过在其列中堆叠所有$N$个切向量来定义。自此,局部坐标系$z$是建立了起来,如何保证这些切向量可以覆盖和表示整个流形的几何呢? 论文给出了正交性的约束条件。
上面我们也有讨论到如果切向空间$\mathcal T_x$在维度上$dim \mathcal T_x$小于流形维度$N$时,这时,切空间下的$N$个切线可能会线性相关,甚至会沿着一些坐标$z$消失, 这就造成了切线空间的崩溃。为了防止崩溃发生,需要加上一个正交条件,$\mathcal T_x$的$N$基础${ \tau_x^j,j=1,…,N }$应该彼此线性独立。 这保证了流形与$N$维欧几里得空间局部“相似”,而不是折叠成具有相关局部坐标的低维子空间。可以在切向量$\tau_x^j$上设置正交条件,即
\[\begin{equation} \langle \tau_x^i,\tau_x^j \rangle = \delta_{ij} \end{equation}\]当$i \neq j$时$\delta_{ij} \neq 0$,当$i=j$时$\delta_{ij} = 1$。为了满足局部性条件,还需要满足$G(x,0) = x$,即局部坐标z的原点应位于x处。 则,满足约束条件为:
(1)局部性:$G(x,0) = x$
(2)正交性:$J_x^T J_x = I_N$,其中$I_N$是大小为N的单位矩阵。
可以将约束条件表示为:
\[\begin{equation} \Omega_{G(x)} = \mu \Vert G(x,0) -x \Vert^2 + \eta \Vert J_x^T J_x - I_N \Vert^2 \end{equation}\]这里的$\mu$和$\eta$为超参,可以控制损失的权重。我们可以理解为这项为正则项,由两个$L_1$损失优化。
训练Localized GAN
文章分析到正则条件的损失表达时,已经算是交代完了Localized GAN。至于训练Localized GAN基本上的思路和普通GAN无异,我们先来看一下Localized GAN 在celebA数据集上训练的模型结构:
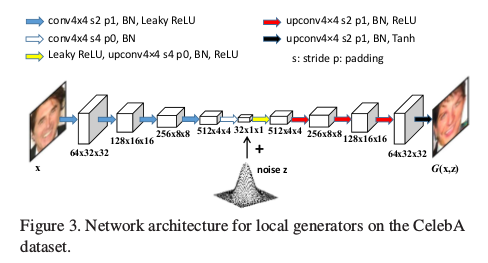
上图主要给出的是生成器$G(x,z)$部分,对于判别器和普通GAN的判别器没有任何差异。对于生成器,前半部分是对数据做流形空间变换,通过噪声$z$和编码向量相加后, 再经过解码得到生成$G(x,z)$。如果训练的数据集的特征空间复杂,也就是流形维度较高时,相应的噪声$z$的维度也要提高,比如CIFAR-10的数据集下论文选用的维度为128。
至于损失函数,整体上和传统GAN类似,对于D:
\[\begin{equation} \max_D \mathbb E_{x \sim P_x} log D(x) + \mathbb E_{x \sim P_x,z \sim P_z} log(1-D(G(x,z))) \end{equation}\]对于G:
\[\begin{equation} \min_G -\mathbb E_{x \sim P_x,z \sim P_z} log D(G(x,z)) + \mathbb E_{x \sim P_x} \Omega_G(x) \end{equation}\]Localized GAN下半监督学习
在分类问题中,感兴趣的函数是分类函数,输出的是数据点的标签。在基于Graph的流形上,可以建立一个分类模型:它输出的分类标签在相似样本上具有最小的变化。 这个就是一种平滑性的假设,是基于图的半监督方法的核心假设。半监督图流形中,常用到Laplacian矩阵来做训练;现在,有了参数化的流形后, 就可以直接定义Laplace-Beltrami算子,从而实现半监督的训练。
这一部分齐国君本人也在他的个人知乎上做了一定的解释,整体上就是Localized GAN可以对流形的局部几何参数化,在数据标签预测上当数据没有标签的半监督下 通过在已有标签下相似样本做出分类决策,从而优化分类器。这部分的详情可以进一步阅读原文, 或者查看齐国君老师的知乎。
Localized GAN实验
实验展示了局部坐标参数化下,可以通过对$z$的各个维度上的变化实现图像的属性和分格的变化,实验在celebA和MNIST数据集下给出了效果展示。
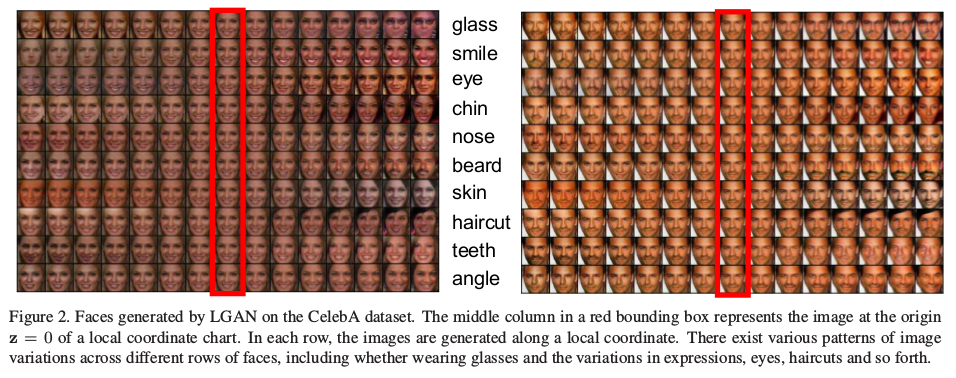

在定量上,论文通过Localized GAN在半监督分类上的效果予以说明:
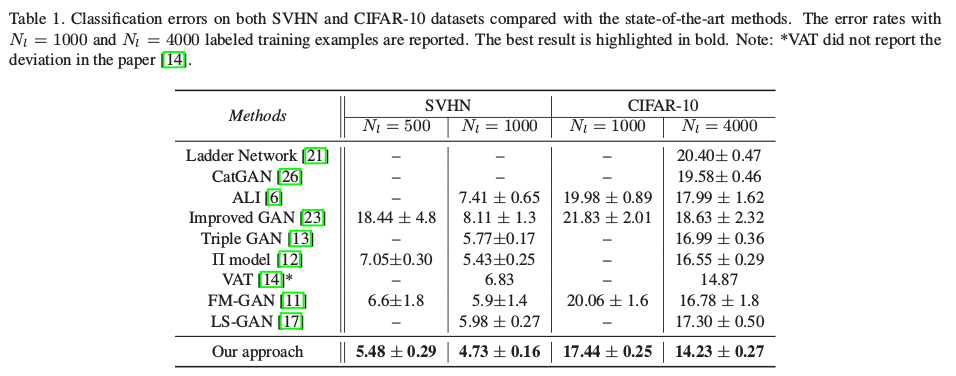
可以看出在半监督分类任务上,Localized GAN展示了最佳的效果。
为了进一步对文章理解,我们参考网上资料,在MNIST数据集上利用Pytorch复现了文章的代码,代码如下:
展示一下,实验的效果图:

总结
论文提出了一种新的Localized GAN模型,该模型使用局部坐标图和相关局部发生器的图集来覆盖整个流形,从而可以捕获流形中局部变换的几何图形。 它还能够从局部坐标直接访问流形结构,无需在传统GAN中反转全局生成器。此外,通过施加切线之间的正交性,它可以防止流形局部塌缩成维度不合理的子空间, 这为解决文GAN的生成多样性不足问题提供了几何洞察。在图像生成和半监督分类任务中展示了优越性能。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










