VAT(虚拟对抗训练)论文解读
2014年5月GAN诞生了,这篇文章中并没有出现Adversarial Trainin这个词,而对抗训练(Adversarial Training) 是在2014年10月被提出。虽然Adversarial Training是在GAN之后被提出,但是这两篇文章都是由Goodfellow创作,而且具体来说Adversarial Training 是包含GAN的。Goodfellow解释为训练一个GAN涉及训练对抗样本的分类器,其中分类器是判别器,对抗样例来自发生器。可以将GAN训练看作是更普遍的对抗训练类别的特例, 在对抗训练下还有很多改进的方案,其中比较知名的是VAT(Virtual Adversarial Training:A Regularization Method for Supervised and Semi-Supervised Learning)简称为虚拟对抗训练, 本文将对VAT作进一步解读。
论文引入
在开始VAT正文阅读前,我们有必要对对抗训练做个了解。说到对抗训练就要提一下对抗样本,对抗样本就是使得机器学习的算法产生误判的样本。我们用一张解释对抗样本最经典的图例说明。

如上图所示,原有的模型以57.7%的置信度判定图片为熊猫,但添加微小的扰动后,模型以99.3%的置信度认为扰动后的图片是长臂猿。这个添加扰动得到的样本, 我们就称之为对抗样本。对抗样本可以让训练优秀的分类网络进行错误的分类,然而人类去看对抗样本的话和真实的样本几乎无异,这也暴露了神经网络的一个弊病。 那么为什么对抗样本会使得网络变得如此脆弱呢?我们看一下诱发这个问题的原因。
Goodfellow认为对于简单的线性模型(x;y),x为真实样本,y为对应的标签,在对x的每个维度添加微小扰动的情况下,扰动的每一个维度上都发生了影响,随着维度的增大, 这个扰动很容易导致最后的输出有较大的变化。对于非线性模型神经网络是因为太“线性”而不能抵抗对抗样本,无论LSTMs, ReLUs, 和maxout网络都设计得很“线性”,所以他们很容易被利用。 我们可以想象一个具有高度线性的网络训练出来的函数,它的高阶导数近似于0,Taylor展开以后占主导作用的是线性部分,所以可以类比为线性分类器。 深度模型之所以在对抗样本的无力最主要的还是由于对抗样本其线性部分的存在。
那如何去构造对抗样本呢?
我们记模型的损失函数为$J(\theta ;x;y)$,其中负梯度方向$− \nabla J_x(\theta ;x;y)$是模型的损失下降最快的方向,那么也就是说负梯度上模型优化最快, 为了使$\hat{x}$对模型的output产生最大的改变,正梯度方向也就是模型梯度下降最慢的方向定为扰动方向,也就是$\nabla J_x(\theta ;x;y)$ 方向上$\hat{x} = x + \epsilon sign(\nabla J_x(\theta ;x;y))$。这里的$\epsilon$为一个超参,控制扰动的选取的界限。
对于模型来说,希望的是预测加入扰动后的结果和真实的一致,这里的损失可以记为:
\[\begin{equation} L_{adv}(x_l, \theta) := D[q(y \vert x_l), p(y \vert x_l + r_{adv}, \theta)] \end{equation}\]这里的$q(y \vert x_l)$为真实数据的预测,$p(y \vert x_l + r_{adv}, \theta)$为加入扰动的预测,D是衡量的标准,这里可以是KL散度。 而对于扰动,则是尽可能的在扰动上使得这两个预测最大化,即:
\[\begin{equation} r_{adv} := \arg \max_{r;\Vert r \Vert leq \epsilon} D[q(y \vert x_l), p(y \vert x_l + r_{adv}, \theta)] \end{equation}\]这个$r_{adv}$无法用封闭形式表达,可以做一下近似处理:
\[\begin{equation} r_{adv} = \epsilon \frac{g}{\Vert g \Vert_2},where g = \triangledown_{x_l} D[h(y;y_l), p(y \vert x_l, \theta)] \end{equation}\]这里的$h(y;y_l)$为$q(y \vert x_l)$的ont-hot表现形式。构造了对抗样本,那么对抗训练如何进行呢?
对抗训练的本质上就是让模型具有较强的鲁棒性,可以抵抗对抗样本的干扰,采用的方式就是生成这些数据,并且把这些数据加入到训练数据中。这样模型就会正视这些数据, 并且尽可能地拟合这些数据,最终完成了模型拟合,这些盲区也就覆盖住了。将对抗样本和原有数据一起进行训练,对抗样本产生的损失作为原损失的一部分, 即在不修改原模型结构的情况下增加模型的loss,产生正则化的效果。
此时目标函数可以表示为:
\[\begin{equation} \widetilde{J}(\theta ,x,y) = \alpha J(\theta ,x,y) + (1 - \alpha)J(\theta ,x+ \epsilon sign(\nabla J_x(\theta ,x,y))) \end{equation}\]VAT则是在对抗训练的基础上,提出了LDS(local distributional smoothness)。VAT提出的LDS也可以理解为在原有模型的基础上加上正则项,这个正则项可以实现局部分布平滑, 也就是不单单关注样本下梯度的扰动(同性噪声),而是对梯度周围进行扰动(各向异性噪声)处理,正因为这样处理,VAT可以不仅仅适用于纯监督环境, 也适用于半监督训练。
总结一下VAT论文的优势:
- VAT在AT的基础上设计了LDS,可以实现局部平滑
- VAT可以实现半监督下模型的对抗训练,并且取得了不错的实验效果
- VAT本身计算上没有太多超参设置,$r_{vadv}$的快速估计提升了计算速度
VAT介绍
VAT整体的设计思路源于对抗训练,然而对抗训练只适用于监督模型的训练,VAT则实现了半监督学习。我们先来规定一下符号,对于标签数据集记为$\mathcal D_l = {x_l^{(n)},y_l^{(n)} \vert n=1,…,N_l}$ 对应的标签就是$y_l$,对于无标签数据集$\mathcal D_{ul} = {x_{ul}^{(m)} \vert m=1,…,N_{ul}}$,训练模型$p(y \vert x,\epsilon)$ 使用的就是标签数据$\mathcal D_l$和无标签数据$\mathcal D_{ul}$。
这里先交代一下VAT实现半监督学习的方法,对于真实数据对应的标签信息分布$q(y \vert x)$在半监督条件下是无法预先获得的,但是只要给定一定标签信息, 在预训练好的模型下得到的分布$p(y \vert x)$接近于真实分布$q(y \vert x_\ast)$($x_\ast$既包含标签数据也包含无标签数据),此时就可以用预测的分布$p(y \vert x)$去替代真实分布$q(y \vert x_*)$。 对于无标签数据,可以采用上一阶段的对unlabel数据的预测结果(logits)作为无标签数据的(虚拟)标签,在虚拟标签上计算对抗方向。文章题目中的虚拟,正是对虚拟标签的放大, 旨在强调模型在半监督条件下的作用。
上述描述对应到算法实现上是对于:
\[\begin{equation} L_{qadv}(x_\ast,\theta) = D[q(y \vert x_*), p(y \vert x_* + r_{qadv},\theta)] \end{equation}\] \[where r_{qadv} := \arg \max_{r;\Vert r \Vert \leq \epsilon} D[q(y \vert x_*), p(y \vert x_*,\theta)]\]这里的$q(y \vert x_\ast)$我们无法获得,但是我们由预训练的模型可以得到$p(y \vert x,\hat{\theta})$,我们就用$p(y \vert x,\hat{\theta})$代替 $q(y \vert x_\ast)$,从而实现半监督下对抗训练的开展。此时,可进一步对上式做变换:
\[\begin{equation} \begin{aligned} & LDS(x_\ast,\theta) := D[p(y \vert x,\hat{\theta}), p(y \vert x_\ast + r_{vadv},\theta)]\\ & r_{vadv} := \arg \max_{r;\Vert r \Vert_2 \leq \epsilon} D[p(y \vert x,\hat{\theta}), p(y \vert x_\ast,\theta)] \end{aligned} \end{equation}\]这就是虚拟对抗扰动,损失$LDS(x_\ast,\theta)$可以被认为是在每个输入数据点x处当前模型的局部平滑度的负测量,并且其减小将使模型在每个数据点处平滑, 对于输入数据点上取LDS的平均:
\[\begin{equation} \mathcal R_{vadv}(\mathcal D_l,\mathcal D_{ul},\theta) := \frac{1}{N_l,N_{ul}} \sum_{x_* \in \mathcal D_l,\mathcal D_{ul}} LDS(x_*,\theta) \end{equation}\]则,VAT整个网络的目标函数可以写为:
\[\begin{equation} \mathcal l(\mathcal D_l,\theta) + \alpha \mathcal R_{vadv}(\mathcal D_l,\mathcal D_{ul},\theta) \end{equation}\]这里的$\mathcal l(\mathcal D_l,\theta)$是有标签数据下的模型损失函数,可以是负的对数似然。$\mathcal R_{vadv}$则作为损失函数的正则化, 在半监督条件下通过对抗训练增强模型对对抗样本的鲁棒性。这里的超参数只有$\epsilon$和$\alpha$。
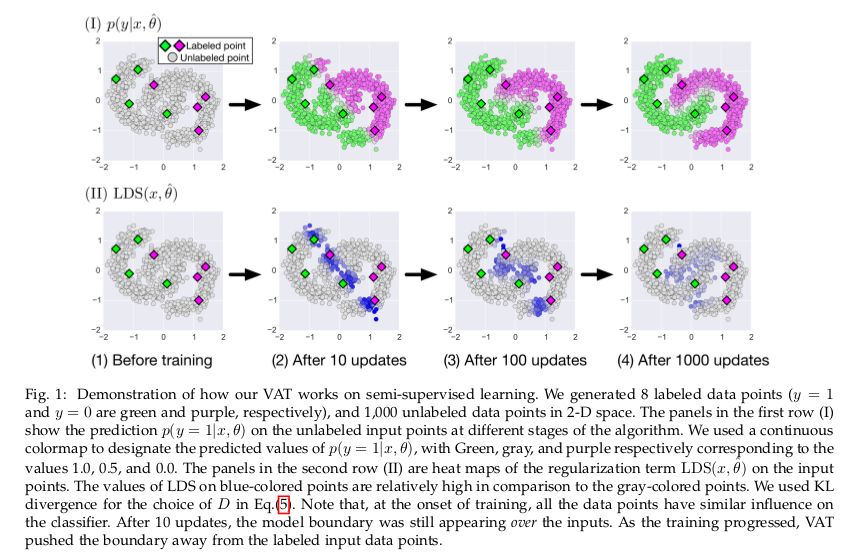
下图显示了VAT如何在二维合成数据集上进行半监督学习。实验使用了一个NN分类器,其中一个隐藏层有50个隐藏单元。在训练开始时,分类器预测同一簇中输入数据点的不同标签, 并且边界上的LDS非常高(训练刚开始时边界)。算法优化模型在具有大LDS值的点周围平滑。随着训练的进行,模型的演变使得具有大LDS值的点上的标签预测受到附近标记输入的强烈影响。 这鼓励模型预测属于同一群集的点集的相同标签,这是在半监督学习中经常需要的。在迭代1000次后,边界已经分的很清晰了,同时预测的标签也是越来越精准。
快速确定$r_{vadv}$值
一旦计算出虚拟对抗扰动$r_{vadv}$此时$LDS(x_\ast,\theta)$的计算就变成了输出分布$p(y \vert x,\hat{\theta})$和$p(y \vert x_\ast + r_{vadv},\theta)$之间的散度D的计算。 然而,$r_{vadv}$的计算不能像原始对抗训练那样使用线性近似(公式3)。因为对于预训练模型$D[p(y \vert x,\hat{\theta}), p(y \vert x_\ast + r,\theta)]$ 在$r=0$时,存在最小值0,对于r的一阶微分也为0,梯度上提供不了有用的信息。
为了便于描述,记$D[p(y \vert x,\hat{\theta}), p(y \vert x_\ast + r,\theta)]$为$D(r,x_\ast,\theta)$。由于最小值0时,一阶微分也为0, 文章采用二阶泰勒展开近似计算:
\[\begin{equation} D(r,x,\theta) = f(0) + f'(0)r + \frac{f''(0)}{2!}r^2 ... \approx \frac{1}{2}r^T H(x,\hat{\theta})r \end{equation}\]这里的$H(x,\hat{\theta})$D的hession矩阵,即$H(x,\hat{\theta}) = \nabla \nabla_r D(r,x,\hat{\theta}) \vert_{r=0}$,此时, $r_{vadv}$作为$H(x, \hat{\theta})$的第一个特征向量$u(x,\theta)$出现,并且值为$\epsilon$ (二次型在单位元上的最大值和最小值分别对应其最大特征值和最小特征值,此时r等于其对应的特征向量,这个具体的证明将Hermite矩阵正交对角化)。 因此,$r_{vadv}$可近似求解为:
\[\begin{equation} \begin{aligned} r_{vadv}(x,\theta) &\approx \arg\max_{r} \{r^TH(x,\theta)r; \Vert r \Vert_2 \leq \epsilon\} \\ &= \epsilon \overline{u(x,\theta)} \end{aligned} \end{equation}\]其中$\overline{.}$表示的是将任意一个非零向量$v$投影为其方向向量对应的单位向量$\overline{v}$。 然而特征值计算是一个$O(I^3)$计算复杂度的过程, 文章采用幂迭代法和有限差分法 来计算$r_{vadv}$。
设$d$是一个随机抽样的单位矢量。 只要$d$不与主特征向量$u$垂直,则迭代计算:
\[\begin{equation} d \gets \overline{Hd} \end{equation}\]此时$d$是收敛到主特征向量$u$的,对于$H$的计算,不需要直接计算$H$,而是近似为有限差分:
\[\begin{equation} \begin{aligned} Hd &\approx \frac{\nabla_r D(r,x,\hat{\theta}) \vert_{r=\xi d} -\nabla_r D(r,x,\hat{\theta})\vert_{r=0}}{\xi} \\ &= \frac{\nabla_r D(r,x,\hat{\theta})\vert_{r=\xi d}}{\xi} \end{aligned} \end{equation}\]此时$d$可表示为:
\[\begin{equation} d \leftarrow \overline{\nabla_r D(r,x,\hat{\theta}) \vert_{r=\xi d}} \end{equation}\]在幂迭代下,这种近似可以由迭代次数K来单调改善,在实验中$K=1$就可以实现较好的结果了,此时,可以对$r_{vadv}$进一步改写为:
\[\begin{equation} \begin{aligned} &r_{vadv} = \epsilon \frac{g}{\Vert g \Vert_2} \\ &where g = \nabla_r D[p(y \vert x,\hat{\theta}), p(y \vert x+r,\hat{\theta})] \vert_{r = \xi d} \end{aligned} \end{equation}\]综合上述分析,我们可以对正则项$\nabla_\theta \mathcal R_{vadv}$的求解做一个梳理,整体思路的伪代码如下:

对于幂迭代次数K,我们可以对VAT的正则项做一个表达:
\[\begin{equation} \mathcal R^{(K)}(\theta ,\mathcal D_l,\mathcal D_{ul}) := \frac{1}{N_l + N_{ul}} \sum_{x \in \mathcal D_l,\mathcal D_{ul}} \mathbb E_{r_K}[D[p(y \vert x,\hat{\theta}), p(y \vert x+r_K,\theta)]] \end{equation}\]对于VAT就是幂迭代次数大于等于1次,即$K \geq 1$。当$K=0$时,也就是不采用幂迭代求解$R_{vadv}$,称这种方法为RPT,RPT是VAT的降级版本, 不执行幂迭代,RPT仅在每个输入数据点周围各向同性地平滑函数。
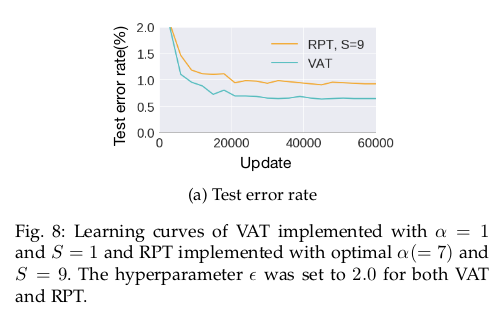
VAT平滑模型的方向比RPT平滑模型的方向更具确定性,模型均匀分布在半径$\epsilon$的范围内,RPT学习的稳定性总是受到$\mathcal R^{(0)}$的方差影响。 后面实验中,文章也对RPT和VAT做了进一步的比较。
VAT实验
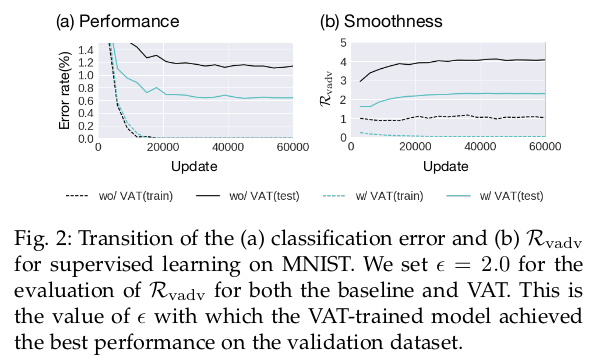
论文实验建立在MNIST,CIFAR-10和SVHN上,这几个数据集想必大家都是很熟悉的,衡量分布的D实验中采用了KL散度实现。在MNIST有监督条件下,论文对比了有无VAT正则的效果, wo指的是无VAT,w指的是加入VAT,下图可以看出无论是错误率还是光滑性VAT都表现了一定的优势:
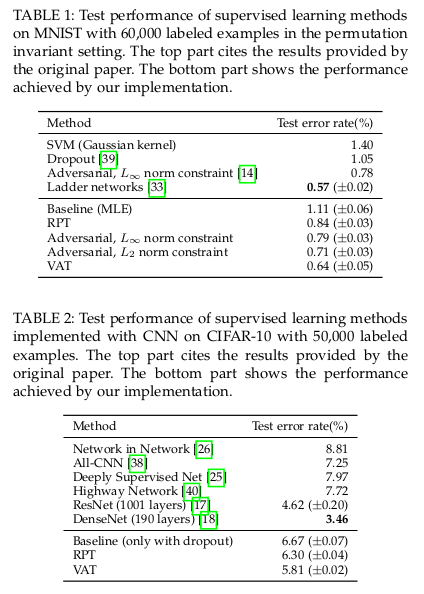
在有监督下定量分析上,VAT也是取得了一定的优势:
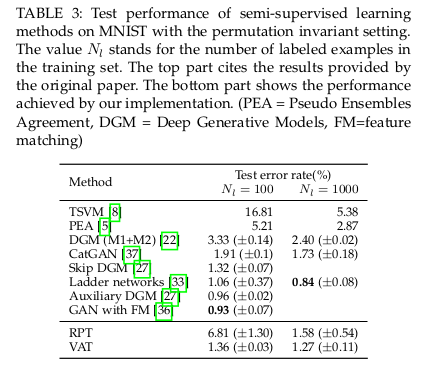
在半监督学习下更是展现了优势:
实验证实,在VAT中加入交叉熵损失可以进一步提高网络性能:

对于VAT涉及的超参数$\alpha$和$\epsilon$的选择,论文做了超参数选择的实验,实验发现$\alpha=1.0$时达到较好的效果。
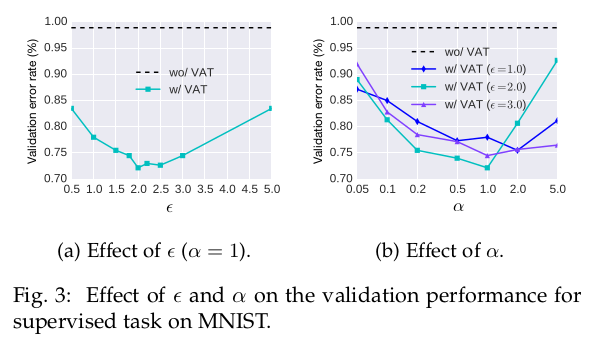
VAT较RPT在之前的定量表格下已经展示了优势,为了进一步比较,论文又做了对比实验:
总结
VAT是在对抗训练的基础上将监督学习模型扩展到半监督学习模型,同时模型在同向噪声鲁棒性提高到可以在异向噪声具有鲁棒性,在监督和半监督条件下都取得不错的实验结果。 快速近似求解$r_{vadv}$,带来了较小的计算成本,模型只有两个超参数。论文实验部分写的很是详细,感兴趣的可以进一步阅读原文了解。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










