Real or not real,GAN真的在对抗中判定了真假?
GAN自提出以来就以生成对抗为目标进行模型优化,这种对抗真的区分了真实数据和生成数据了吗?ICLR2020中的一篇Real or Not Real, that is the Question(RealnessGAN)提出了对传统GAN判别数据真假的质疑,文章抛出了在传统GAN中对于判别器的鉴别输出为一常数score是不合理的观点,并由此提出合理的解决方案,本文将对RealnessGAN进行解析,探究GAN是否真的区分了真假。
论文引入
GAN[1]自提出就得到了空前反响,GAN在逼真的图像生成方面以及处理高维数据时的灵活性上推动着包括图像,音频和视频生成的发展,更甚者在诸如强化学习、迁移学习等也展示了一定的价值。GAN通过生成器和判别器的博弈下达到交替更新,其核心就是模型能否鉴别数据的真实与生成并与生成器形成对抗。
在标准的GAN中,输入样本的真实性由判别器使用单个标量估算,也就是判别输出的是一个鉴别分数。然而诸如图像之类的高维数据,需要从多个角度认知它们,并基于多个标准来推断这幅图像是否逼真。 如图1所示,在拿到一张人脸肖像图时,我们可能会关注其面部结构,皮肤色调,头发纹理,甚至虹膜和牙齿等细节,它们每一个属性都代表着真实性的不同方面。 此时判别器用单个标量输出鉴别结果,这是多个量度的抽象和汇总,它们共同反映了图像的整体真实性。 但是这种简洁的测量可能传达的信息不足,无法引导生成器向着正确的图像进行生成,这就可能导致在GAN中众所周知的模式崩溃和梯度消失的发生。

图1.人脸肖像图中的人眼感知(a)真实人眼感知(b)由于面部结构/组件不协调,背景不自然,样式组合异常和纹理变形可能降低的真实感
既然判别器的单标量输出是不合理的,那么怎样表示判别器的输出呢?RealnessGAN提出了通过将逼真度视为随机变量,也就是对于判别器的输出表示为一分布而不是单个标量。整体的架构和训练上RealnessGAN沿用标准GAN的方式,只是将判别器的输出表示为一个分布,并且在优化阶段是以分布进行度量。总结一下RealnessGAN的优势:
- 将标量真实性得分扩展为分布的真实性得分,判别器$D$为生成器$G$提供了更强的指导。
- RealnessGAN的思路可以推广到一般的GAN中,具有较强的灵活性。
- 基于一个简单的DCGAN架构,RealnessGAN可以成功地从头开始学习生成$1024 \times 1024$分辨率的逼真的图像。
RealnessGAN原理分析
在RealnessGAN原理分析前,先回顾一下标准GAN的优化过程:
\[\begin{equation} \begin{aligned} \min_G\max_DV(G,D)&=\mathbb E_{x \sim p_{data}}[\log D(x)]+E_{z \sim p_z}[\log (1−D(G(z)))] \\ &= \mathbb E_{x \sim p_{data}}[\log D(x)-0]+E_{x \sim p_g}[\log(1−D(x))] \end{aligned} \end{equation}\]此时用0和1分别表示两个虚拟的标量,也就是作为判别器的输出对照,判别器鉴定真实为1,虚假为0。通过固定的$G$,最优$D$得到$D_G^∗(x)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$,再将$D$固定为最优值,最优$G$满足$p_g=p_{data}$。
采用单个标量作为真实性的度量是受限的,现实中的很多本质上是一个涵盖多个因素的随机变量,此时RealnessGAN便发挥了作用,用一个分布$p_{realness}$替换判别器$D$的标量输出,那么对于一个输入$x$,此时$D(x)={ p_{realness}(x, u);u\in\Omega }$其中$\Omega$是输出$p_{realness}$的结果集,可以将每个结果$u$视为通过某些标准估算的真实性度量。既然判别器的输出被规定为是个分布,那么如何去优化这个判别器输出呢?
类似于标准GAN的0和1真假标量,RealnessGAN需要两个分布来代表判别器输出的真实和虚假图像的鉴定分布,这里的分布可不同于数据的分布,这里的分布指的是判别器的对照分布。定义两个分布$\mathcal A_1$表示理论上的判别输出为真实的分布,$\mathcal A_0$表示理论上的判别输出为假的分布,它们也在$\Omega$上定义,优化分布之间的距离可以想到的是通过KL散度进行,此时生成器与判别器的博弈过程表示为:
\[\max_G\min_DV(G,D)= \mathbb E_{x \sim p_{data}}[\mathcal D_{KL}(\mathcal A_1 \Vert D(x))]+E_{x \sim p_g}[\mathcal D_{KL}(\mathcal A_0 \Vert D(x))]\]先从理论角度分析下这个目标函数,对于判别器$D$,它的目的是为了将真的数据鉴定为真的,假的数据鉴定为假的,所以对于真实数据$x\sim p_{data}$,希望鉴定结果$D(x)$与理论真实分布$\mathcal A_1$尽可能接近,即$\mathcal D_{KL}(\mathcal A_1 \Vert D(x))=0$为理想解,同理对于生成数据$x \sim p_g$则希望判别输出与理论虚假分布$\mathcal A_0$尽可能接近,即$\mathcal D_{KL}(\mathcal A_0 \Vert D(x))=0$为理想解。而对于生成器$G$,公式的第一项由于没有$G$的参与不允讨论,而对于第二项生成器则希望能够骗过判别器,即$\mathcal D_{KL}(\mathcal A_0 \Vert D(x))$越大越好,也就是希望$D(x)$与理论虚假分布$\mathcal A_0$差异越大越好。那生成数据的判别分布于理论虚假分布差异越大,怎么能保证与理论真实分布$\mathcal A_1$越接近呢?文章也进行了讨论,主要通过对生成器的损失进行调整实现,这个我们后面再详细说明。
知道了目标函数,那怎么保证模型博弈到最后得到的最优解就是$p_g=p_{data}$呢?这需要进一步对目标函数进行分析了,接下来会有一定的公式推导,不喜欢这部分的可以直接跳到下一节,最后的结论就是模型的收敛最优解就是生成数据分布于真实数据分布相同$p_g=p_{data}$。
与标准GAN的分析相同,固定$G$,目标$D$表示为:
\[\begin{equation} \begin{aligned} \min_DV(G,D) &= \mathbb E_{x \sim p_{data}}[\mathcal D_{KL}(\mathcal A_1 \Vert D(x))]+E_{x \sim p_g}[\mathcal D_{KL}(\mathcal A_0 \Vert D(x))]\\ &= \int_x (p_{data}(x) \int_u \mathcal A_1(u) \log \frac{\mathcal A_1(u)}{D(x,u)}du + p_{g}(x) \int_u \mathcal A_0(u) \log \frac{\mathcal A_0(u)}{D(x,u)}du)dx \\ &= \int_x p_{data}(x) \int_u \mathcal A_1(u) \log \mathcal A_1(u)dudx + \int_x p_{g}(x) \int_u \mathcal A_0(u) \log \mathcal A_0(u)dudx\\ &- \int_x \int_u (p_{data}(x)\mathcal A_1(u)+p_g(x)\mathcal A_0(u)) \log D(x,u)dudx \end{aligned} \end{equation}\]根据熵的定义,记$h(\mathcal A_1)=-\int_u \mathcal A_1(u) \log \mathcal A_1(u)du$,同理$h(\mathcal A_0)=-\int_u \mathcal A_0(u) \log \mathcal A_0(u)du$,则上式改写为:
\[\begin{equation} \begin{aligned} \min_DV(G,D) &= \int_x (p_{data}(x)h(\mathcal A_1)+p_g(x)h(\mathcal A_0))dx - \int_x \int_u (p_{data}(x)\mathcal A_1(u)+p_g(x)\mathcal A_0(u)) \log D(x,u)dudx \end{aligned} \end{equation}\]公式的第一项与$D$无关,将之记为$C_1$,上式可进一步表示为:
\[\begin{equation} \begin{aligned} \min_DV(G,D) &= - \int_x(p_{data}(x)+p_g(x))\int_u \frac{p_{data}(x) \mathcal A_1(u)+p_g(x)\mathcal A_0(u)}{p_{data}(x)+p_g(x)}\log D(x,u)dudx + C_1 \end{aligned} \end{equation}\]记$p_x(u) =\frac{p_{data}(x) \mathcal A_1(u)+p_g(x)\mathcal A_0(u)}{p_{data}(x)+p_g(x)} $,$C_2=p_{data}(x)+p_g(x)$,可得到:
\[\begin{equation} \begin{aligned} \min_DV(G,D) &= C_1 + \int_xC_2 (-\int_u p_x(u)\log D(x,u)du - h(p_x) + h(p_x))dx \\ &= C_1 + \int_xC_2 (-\int_u p_x(u)\log D(x,u)du + \int_u p_x(u) \log p_x(u) + h(p_x))dx \\ &= C_1 + \int_x C_2 \mathcal D_{KL}(p_x \Vert D(x))dx + \int_x C_x h(p_x) dx \end{aligned} \end{equation}\]最小化\(V(G,D)\)就是最小化\(D_{KL}(p_x \Vert D(x))\),则D的最优解就是\(D^*(x) ={p_x}\),接下来就是对$G$的最优解进行讨论,当\(D^*(x) =p_{x}\)时,假设\(p_g=p_{data}\),此时\(D_G^*(x,u)=\frac{\mathcal A_1(u) + \mathcal A_0(u)}{2}\),则对应的\(V^*(G,D^*_G)\):
\[V^⋆(G,D_G^⋆)=\int_u \mathcal A_1(u) \log \frac{2 \mathcal A_1(u)}{\mathcal A_1(u)+ \mathcal A_0(u)} + \mathcal A_0(u) \log \frac{2 \mathcal A_0(u)}{\mathcal A_1(u)+ \mathcal A_0(u)}du\]从\(V(G,D_G^*)\)中减去\(V^*(G,D^*_G)\)得:
\[\begin{equation} \begin{aligned} V^\prime(G,D_G^*)&=V(G,D_G^*)-V^*(G,D^*_G)\\ &=\int_x \int_u (p_{data}(x)\mathcal A_1(u)+p_g(x)\mathcal A_0(u)) \log \frac{(p_{data}(x)+p_g(x))(\mathcal A_1(u)+ \mathcal A_0(u))}{2(p_{data}(x)\mathcal A_1(u)+p_g(x)\mathcal A_0(u))}dudx \\ &= -2\int_x \int_u \frac{p_{data}(x)\mathcal A_1(u)+p_g(x)\mathcal A_0(u)}{2} \log \frac{\frac{p_{data}(x)\mathcal A_1(u)+p_g(x)\mathcal A_0(u)}{2}}{\frac{(p_{data}(x)+p_g(x))(\mathcal A_1(u)+ \mathcal A_0(u))}{4}}dudx \\ &= -2 \mathcal D_{KL}(\frac{p_{data}\mathcal A_1 + p_g \mathcal A_0}{2} \Vert \frac{(p_{data}+p_g)(\mathcal A_1+ \mathcal A_0)}{4}) \end{aligned} \end{equation}\]由于\(V^*(G,D^*_G)\)相对于$G$为常数,最大化\(V(G,D_G^*)\)等价于最大化\(V^\prime(G,D_G^*)\),当且仅当KL散度达到其最小值时,才能获得最佳\(V^\prime(G,D_G^*)\),对于任何有效的$x$和$u$:
\[\frac{p_{data}\mathcal A_1 + p_g \mathcal A_0}{2} = \frac{(p_{data}+p_g)(\mathcal A_1+ \mathcal A_0)}{4}\]即$(p_{data}-p_g)(\mathcal A_1 - \mathcal A_0)=0$,因此,只要存在一个有效的$u$,使得$\mathcal A_1(u) \ne \mathcal A_0(u)$,对于任何有效$x$,都有$p_{data} = p_g$。
RealnessGAN的实施和训练
当满足$\mathcal A_1(u) \ne \mathcal A_0(u)$,为了优化模型,此时的$G$需要足够的强大才能匹配理论真实分布,随着$u$数量的增加,对$G$施加的约束因此变得更加严格,则$G$需要付出更多去学习才能匹配判别下理论真实分布,所以$u$数量的增加决定着模型的一定性能,说了这么多,这个$\mathcal A_1$和$\mathcal A_0$以及$u$到底怎么表示呢?
我们知道$\mathcal A_1$和$\mathcal A_0$是定义下的判别理论分布,只要这两个分布之间差异足够的大即可,那么到底取什么呢?这个答案在文章公布的源码中作者规定了理论判别真实分布锚点$\mathcal A_1$和理论判别虚假分布锚点$\mathcal A_0$。
# e.g. normal and uniform
gauss = np.random.normal(0, 0.1, 1000)
count, bins = np.histogram(gauss, param.num_outcomes)
anchor0 = count / sum(count)
unif = np.random.uniform(-1, 1, 1000)
count, bins = np.histogram(unif, param.num_outcomes)
anchor1 = count / sum(count)
对于理论判别真实分布$\mathcal A_1$,作者用$(-1,1)$的均匀分布来表示,用均值为0,方差为0.1的高斯分布来表示理论判别虚假分布$\mathcal A_0$,通过np.histogram通过对这采样的1000个点进行num_outcomes的离散化,这个num_outcomes就是$u$的数量。高斯分布与均匀分布分布上的差异决定着锚点$\mathcal A_1$与$\mathcal A_0$的不同,这也满足了推导的条件,num_outcomes则在一定程度上影响着生成的结果,这点我们在后面的实验中再进行分析。
回到之前提到的优化$G$的问题上来,上述的目标函数对于$G$而言是通过欺骗$D$是增大假样本的$D(x)$和锚点分布$\mathcal A_0$之间的KL散度,而不是减小假样本和锚点分布$\mathcal A_1$之间的KL散度,作者进行了损失上的一定改进,对于一般$G$的优化:
\[(G_{object1}) \min_G -\mathbb E_{z \sim p_z}[\mathcal D_{KL}(\mathcal A_0 \Vert D(G(z)))]\]文章又提出了:
\[(G_{object2}) \min_G \mathbb E_{x \sim p_{data},z\sim p_z}[\mathcal D_{KL}(D(x) \Vert D(G(z)))] -\mathbb E_{z \sim p_z}[\mathcal D_{KL}(\mathcal A_0 \Vert D(G(z)))]\] \[(G_{object3}) \min_G \mathbb E_{z\sim p_z}[\mathcal D_{KL}(\mathcal A_1 \Vert D(G(z)))] -\mathbb E_{z \sim p_z}[\mathcal D_{KL}(\mathcal A_0 \Vert D(G(z)))]\]至于说哪个损失更好用,这个在实验中进行了对比。值得一说的是RealnessGAN提出的思想可以用在大部分的GAN中,只需要对损失函数进行一定的调整即可,这也展示了RealnessGAN的灵活性。
在训练阶段,采用Adam优化器,BN用在生成器,SN用在判别器。
实验
文章首先进行了简单的实验验证模型的有效性,通过toy dataset进行验证,与基准模型进行了对比,选取了StdGAN[2]、WGAN-GP[3]、LSGAN[4]和HingeGAN[5]作为基准模型,得到的结果如图2所示。
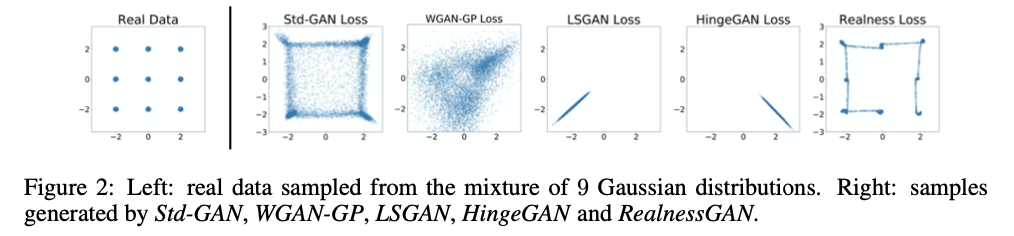
图2.toy dataset下RealnessGAN与基准模型的对比
可以看到RealnessGAN展示了较为优越的结果生成,在验证$u$的数量上,文章也进行了实验,得到的结果如图3所示。
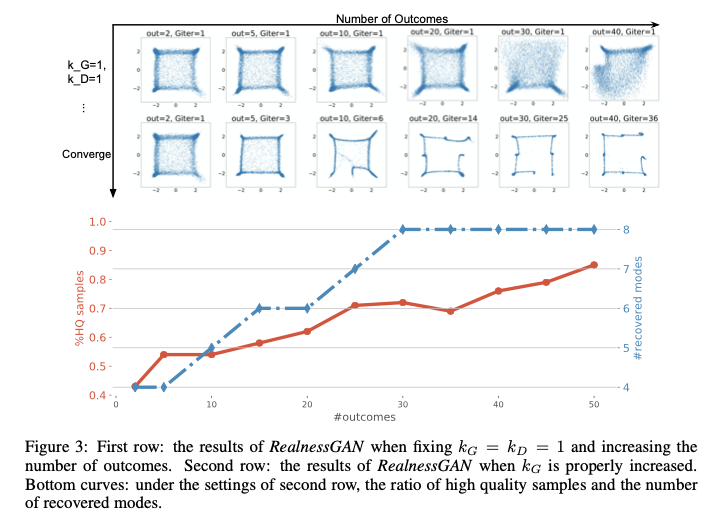
图3.输出结果数量对生成的影响
在固定$G$的更新数量下,$u$的数量越多并没有取得越好的结果,但是随着$G$给予足够的更新,$u$的数量增大得到的结果就越有优势。在定性上模型给出的结果如图4.

图4.RealnessGAN在Cifar10、CelebA和FFHQ下的生成结果。
定量上文章在Cifar10数据集下进行了对比实验:
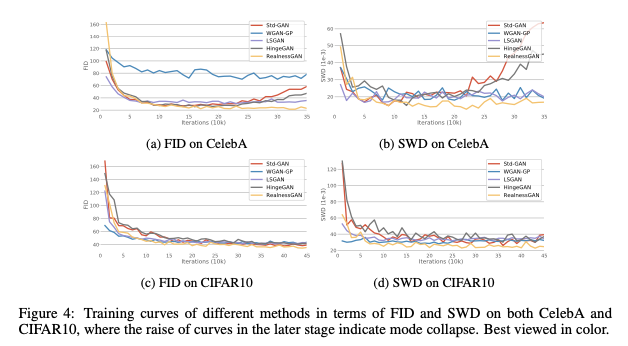
图5.在Cifar10数据集下各模型在FID和SD指标下结果。
为了验证$\mathcal A_1$与$\mathcal A_0$的差异性对结果的影响,文章做了对比实验,结果如图6.
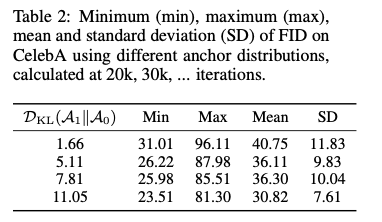
图6.锚点分布的差异性对生成结果的影响,
对于$G$的损失优化上,作者进行了比对。
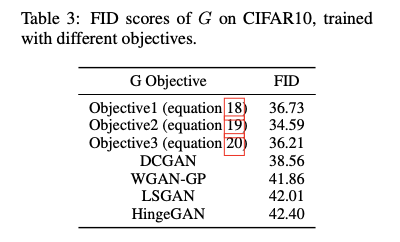
图7.G的不同损失下的生成结果。
总结
RealnessGAN从分布的角度扩展了生成对抗网络的逼真性,以判别输出分布替代了标准GAN中的单标量判别输出,此时判别器会从多个角度估算真实性,从而为生成器提供更多信息指导。同时这种判别输出分布的方式可以推广到更多的一般性GAN的训练上,从理论和实验分析上可以得到该方法的有效性,对于GAN的发展起到了推助作用。
参考文献
[1] Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4681-4690.
[2] Zhang Z, Yu J. STDGAN: ResBlock Based Generative Adversarial Nets Using Spectral Normalization and Two Different Discriminators[C]//Proceedings of the 27th ACM International Conference on Multimedia. 2019: 674-682.
[3] Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein gans[C]//Advances in neural information processing systems. 2017: 5767-5777.
[4] Mao X, Li Q, Xie H, et al. Least squares generative adversarial networks[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 2794-2802.
[5] Junbo Zhao, Michael Mathieu, and Yann LeCun. Energy-based generative adversarial network. In ICLR, 2017.










