SN-GAN论文解读
GAN自诞生到现在一直面临着模型训练不稳定的问题,尽管已经有很多方法在极力控制着GAN训练的稳定,但是都没有从根本上解决这个问题。 实验中的Trick,损失函数的变换,正则化的引入等等都是解决GAN训练不稳定的方法,SN-GAN利用谱归一化的方法, 使得GAN满足Lipschitz假设,从而让模型更加稳定。
论文引入
GAN训练不稳定应该是GAN实现逼真图像生成中美中不足的地方了。归根结底的去讨论到底是什么问题造成GAN训练不稳定的?这个估计很难给出一个具体的答案, 但是源头上分析还是GAN的生成器和判别器是交替更新,内部存在对抗导致的。原始GAN中讨论最多的就是当判别器训练的很好时,生成器的参数容易造成梯度消失。 严格的数学推导可移步这里查看,虽然WGAN、 LSGAN等在损失函数上对GAN做了改进,但是还是存在训练不稳定的情况。
WGAN利用Wasserstein距离代替原始GAN中的JS距离,但是为了去衡量Wasserstein距离判别器必须要满足Lipschitz假设,Lipschitz就是让模型对输入的细微变化不敏感, 用数学角度阐述就是对于$f(x)$在$x$处的导数要很小,小到什么程度呢?用K去衡量$\vert f(x_1) - f(x_2) \vert \leq K \vert x_1 - x_2 \vert $ 为了满足这个假设,在WGAN中是直接对判别器的参数做裁剪,迫使参数在$[-c,c]$之间,这种操作的方法算是改变了权值矩阵的最大奇异值,多少会造成信息损耗。 虽然WGAN-GP采用梯度惩罚达到Lipschitz假设,这个梯度惩罚并非作用于全网络下,仅仅是在真假分布之间抽样处理。
Lipschitz假设对于判别器D是很重要的,因为Lipschitz假设可以限制住判别器的函数空间,一旦D的函数空间优化的太大,生成样本将会很容易判别必定导致 模型训练的不稳定(我们后续给出详细说明)。GAN就是为了让D和G在对抗中和谐下去,不希望看到一方过于强大。实现Lipschitz假设除了WGAN和WGAN-GP的方法外,还可以采用 weight norm,它是对矩阵的行向量做L2 norm,本质是规范化矩阵所有奇异值的总和,但是对整体奇异值做优化,毫无例外都会破坏奇异值结构,导致信息损失。
SN-GAN采用谱归一化的思想去让判别器D满足Lipschitz假设,整体上SN-GAN只改变权值矩阵的最大奇异值,因此可以最大程度保留权值矩阵的原始信息, 并且还可以做到K-Lipschitz正则。对SN-GAN的优势总结一下:
- Lipschitz常数K是唯一要调整的超参数,只改变权值矩阵的最大奇异值
- 实施简单,额外的计算成本很小
Lipschitz假设对GAN的重要性
对于输入为$x$的判别器网络可以表示为:
\[f(x,\theta) = W^{L+1} a_L (W^L(a_{L-1}(W^{L-1}(\cdots a_1(W^1x) \cdots))))\]其中,$\theta:= \lbrace W^1, \cdots, W^L, W^{L+1} \rbrace$是学习参数集,也就是网络的权重,$a_l$是非线性激活函数,上述表达式没有考虑偏差。 完整的判别器网络可以表示为:
\[D(x,\theta) = \mathcal A(f(x,\theta))\]对于GAN而言,判别器的目的是为了区分开真假样本,要最大化目标函数$max_D V(G,D)$,在固定生成器后得到的判别器最优解为:
\[D_G^*(x) = \frac{q_{data}(x)}{q_{data}(x) + p_G(x)} = sigmoid(f^*(x))\]我们知道$sigmoid$的表达式为$\frac{1}{1+e^{-x}}$代入上式可以解出:
\[f^*(x) = log q_{data}(x) - log p_G(x)\]我们对$f^*(x)$对$x$求导:
\[\nabla_x f^*(x) = \frac{1}{q_{data}(x)} \nabla_x q_{data}(x) - \frac{1}{p_G(x)} \nabla_x p_G(x)\]这个导数可以是无限的,甚至是无法计算的,这就会造成判别器失控(一路无限制优化),导致函数空间很大,这就使得D的能力过强,GAN的平衡倾斜。 为了给予判别器于一定限制,这就要Lipschitz假设,通过添加在输入示例x上定义的正则化项来控制鉴别器的Lipschitz常数,此时优化就为:
\[argmax_{\Vert f \Vert_{Lip} \leq K} V(G,D)\]自此,我们看到Lipschitz假设对于GAN的重要性,为了较好实现Lipschitz假设,谱归一化将展示强大的能力。
谱归一化
Spectral Norm是在SN-GAN之前提出的,SN-GAN将其引入到GAN下。我们这里说的谱归一化是按照SN-GAN 实现思想下的,整体思想就是让模型对输入的细微变化不敏感,也就是最小化:
\[\frac{\Vert f_\Theta(x+\xi) - f(x) \Vert_2}{\Vert \xi \Vert_2} = \frac{(W_{\Theta , x}(x + \xi) + b_{\Theta , x}) - (W_{\Theta , x}(x) + b_{\Theta , x}) \Vert_2}{\Vert \xi \Vert_2} = \frac{\Vert W_{\Theta , x} \xi \Vert_2 }{\Vert \xi \Vert_2} \leq \sigma (W_{\Theta , x})\]此处的$\sigma (W_{\Theta , x})$就是谱归一化的处理,要想保证导数尽可能小就是最小化$\frac{\Vert W_{\Theta , x} \xi \Vert_2 }{\Vert \xi \Vert_2}$ 转而是为了最小化上界 $\sigma (W_{\Theta , x})$,此时对于权值矩阵$A$,且$A \in \mathbb R^{m \times n}$,目标变为:
\[\sigma (A) = \max_{\xi \in \mathbb R^{n},\xi \neq 0} \frac{\Vert A \xi \Vert_2}{\Vert \xi \Vert_2}\]在SN-GAN中将$\xi$理解为网络的每一层$g$下$h_{in} \mapsto h_{out}$此时谱归一化就为最大化:
\[\sigma (A) = \max_{h: h \neq 0} \frac{\Vert Ah \Vert_2}{\Vert h \Vert_2} = \max_{\Vert h \Vert_2 \leq 1} \Vert Ah \Vert_2\]这个就是求矩阵的最大奇异值,对于每一层$g$输入$h$时,对应$g(h) = Wh$根据范数的性质有$\Vert g_1 \circ g_2 \Vert_{Lip} \leq \Vert g_1 \Vert_{Lip} \cdot \Vert g_2 \Vert_{Lip}$
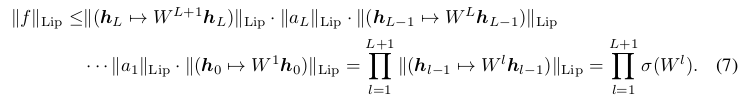
谱归一化的目的就是为了归一化权重矩阵$W$的谱范数,使其满足Lipschitz约束,$\sigma(W)= 1$:
\[\hat{W_{SN}}(W) := W/\sigma(W)\]如果对于判别器D的每层权重$W$都做如上所示的谱归一化,即可将其Lipschitz范数约束在1以下,这个可以从公式(7)中将$W$代入,$\Vert f \Vert_{Lip}$ 的上界为1。这样就达到了限制判别器D的Lipschitz范数的效果,这也就是谱归一化的实现。
文章的2.3节通过对梯度分析,得出相对常规的GAN,谱归一化后的GAN引入了新的正则项,该正则项防止W的列空间在训练中只关心一个特定的方向, 与此同时其防止D中每层的转换对某一个方向敏感。
对于每层的频谱范数$\sigma(W)$是$W$的最大奇异值。 如果用奇异值分解来计算每一轮的$\sigma(W)$,则该算法的计算量特别大。文章采取了power iteration 的方法。实现算法如下:

在作者给的源码中iteration默认为1,但是却实现了最大奇异值的求解,power iteration方法的收敛速度跟矩阵的最大特征值的占优密切相关, 理论上来说只迭代一次是不可能收敛的。但是,注意到两点,1.算法里面复用了$u,v$。2.随机梯度下降更新使得矩阵变化很小。 因此,可以假设微小的更新使得矩阵的最大特征值几乎不变。每次更新复用$u,v$的时候,可以近似为power iteration 的迭代过程,最终达到收敛。
对于整体的损失函数,SN-GAN采用Hinge Loss。
实验
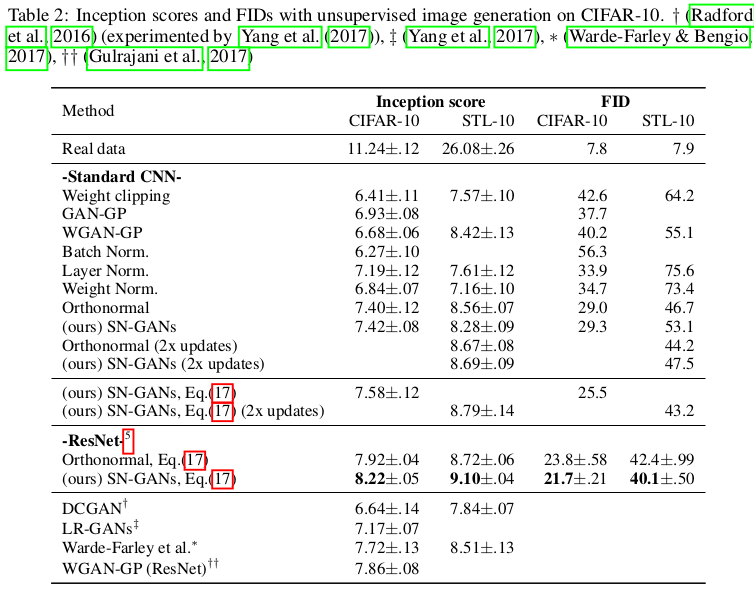
文章在CIFAR-10和STL-10数据集上实验,采用的评价指标分别是Inception Score和Fréchet inception distance(FID)。实验首先在各个GAN模型上 进行对比试验,并且通过多组参数设置验证模型的鲁棒性。
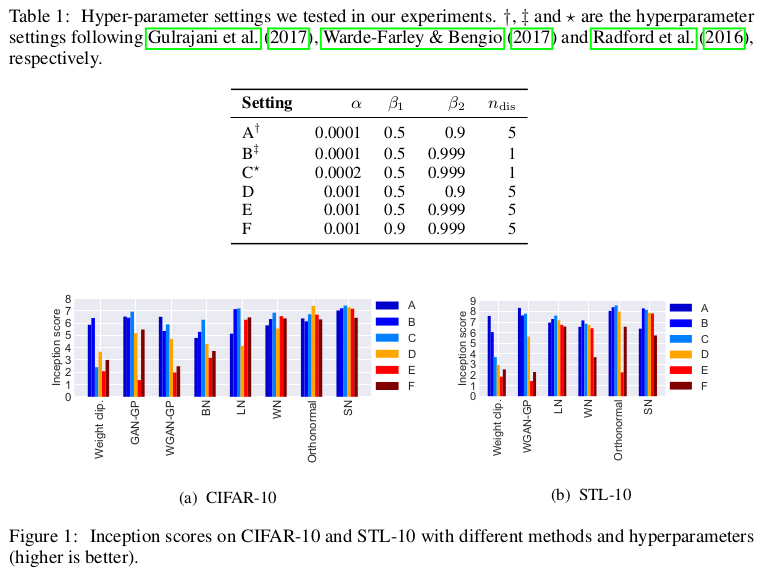
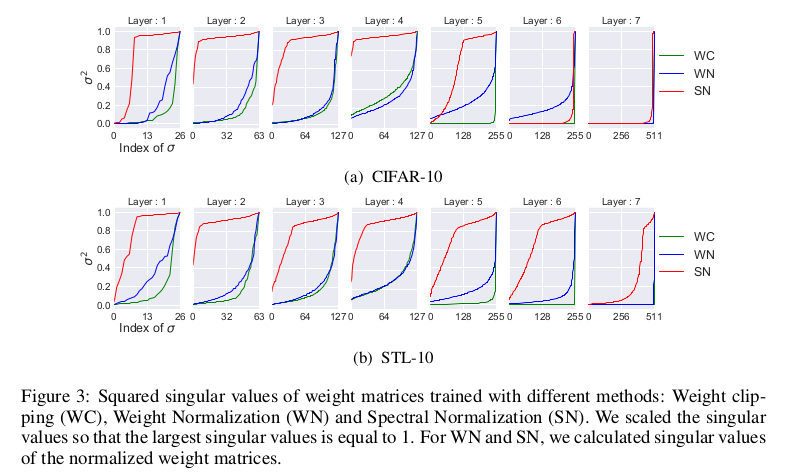
为了证实SN-GAN可以使得权重不只关心一个方向,于是其分析了,在不同的归一化情况下得到的最优化的GAN中,判别器D中权重的分布情况,实验结果图中, 所有的权重都被归一化到了$[0,1]$区间中,从图中可以清晰的看出,采用谱标准化优化产生的D,其中的权重的数值分布较为广泛,并且具有多样性。
为了进一步和正交归一化方法进行比较,文章又做了进一步实验,增加最后一层特征图的维度,用Inception Score来度量两者的性能差别。
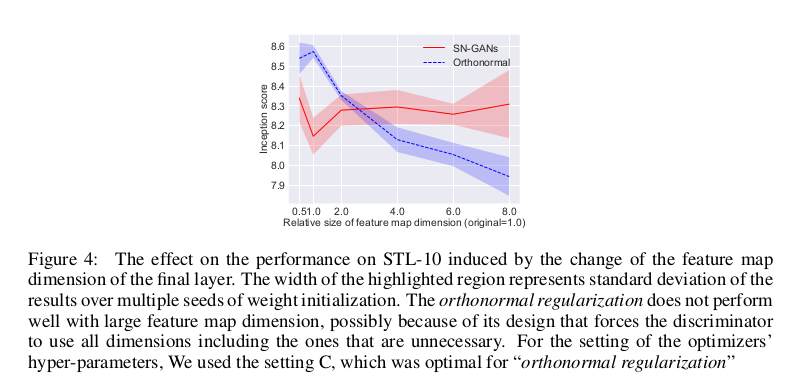
最后实验在ImageNet上做生成,生成效果还是很不错的。

总结
SN-GAN提出谱归一化作为GAN训练的稳定器。在图像生成任务中对GAN应用谱归一化时,生成的示例比传统的权重归一化更加多样化,并且相对于先前的研究获得更好或相近的Inception Score。 该方法对判别器施加全局正则化,而不是由WGAN-GP引入的局部正则化,并且可以组合使用。SN-GAN中的谱归一化对于稳定GAN起到了一定的作用, 在后续GAN的发展上可以以此来增加训练的稳定程度。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










