LS-GAN(损失敏感GAN)介绍
LS-GAN(损失敏感GAN)是由齐国君教授创作的,我感觉可以和WGAN相提并论,也是一篇好文章。今天我们一起来看看这篇文章。
齐国君教授写的Loss-Sensitive GAN。这篇文章算是自己开创了一个新的GAN领域,不过创作的初衷也主要 是为了解决传统GAN存在的在判别器训练很好的情况下,生成器的梯度会发生消失的问题。LS-GAN在文章中分别对比了传统GAN和WGAN,并且在WGAN的基础 上对一些公式做了定量分析和推证,这样让LS-GAN的思想更加的清晰,但是大量的数学公式也是让人读得吃力。
文章指出传统GAN的作者Goodfellow做了一个很大胆的假设:用来评估样本真实度的Discriminator网络具有无限的建模能力,也就是说不管真实样本和 生成的样本有多复杂,判别器都能把它们区分开,这个假设也称为非参数假设。在WGAN中已经推证了在高维样本中,生成样本和真实样本之间的重叠没有即 使存在也可以忽略不计由此带来的就是生成器的损失函数中JS散度为一个常数,从而导致损失函数的值为0引起梯度消失的情况。
无限建模能力是造成梯度消失得一个重要的问题,作者围绕这个思想创造了LS-GAN,直接通过限定GAN的建模能力,得到一种新的GAN模型。这篇文章的数学
公式以及推导也是十分的繁琐和复杂,我就在已有数学的基础上对一些公式做出分析。公式1为LS-GAN的目标函数,这个是用来学习损失函数的目标函数,
通过最小化这个目标得到一个“损失函数”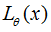 ,
,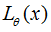 在真实样本上越小
越好,在生成的样本上越大越好。
在真实样本上越小
越好,在生成的样本上越大越好。
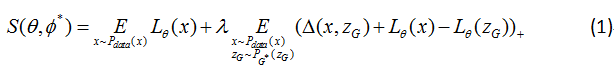
对应的G-网络,通过最小化公式2训练网络:
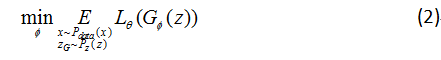
分析上述公式,对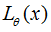 的学习目标S中的第二项
的学习目标S中的第二项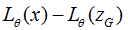 ,它是以真实样本x
和生成样本Zg的一个度量
,它是以真实样本x
和生成样本Zg的一个度量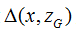 为各自
为各自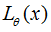 的目标间隔从而把x和Zg分开。
这样的好处是如果生成的样本和真实样本已经很接近,那么就不必要求他们的
的目标间隔从而把x和Zg分开。
这样的好处是如果生成的样本和真实样本已经很接近,那么就不必要求他们的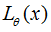 非得有个固定间隔,因为这个时
候生成的样本已经非常好了,已经接近或者达到了真实样本水平。此时LS-GAN就可以集中力量提高那些距离真实样本还很远,真实度不那么高的样本上了。
这样就可以更合理使用LS-GAN的建模能力,一旦限定了建模能力后,也不用担心模型的生成能力有损失了,文章称之为“按需分配”。
非得有个固定间隔,因为这个时
候生成的样本已经非常好了,已经接近或者达到了真实样本水平。此时LS-GAN就可以集中力量提高那些距离真实样本还很远,真实度不那么高的样本上了。
这样就可以更合理使用LS-GAN的建模能力,一旦限定了建模能力后,也不用担心模型的生成能力有损失了,文章称之为“按需分配”。
下图展示了LS-GAN的按需分配的情况,由图我们可以看到当生成的样本绿色的点和真实的样本红色的点分布上在某一部分很相近时,通过目标函数的作用, 将减小离真实样本很近的那一部分分布的训练从而将训练集中在离真实样本较远分布的生成样本的训练上,这样的“按需分配”将大大提高训练的有效性。
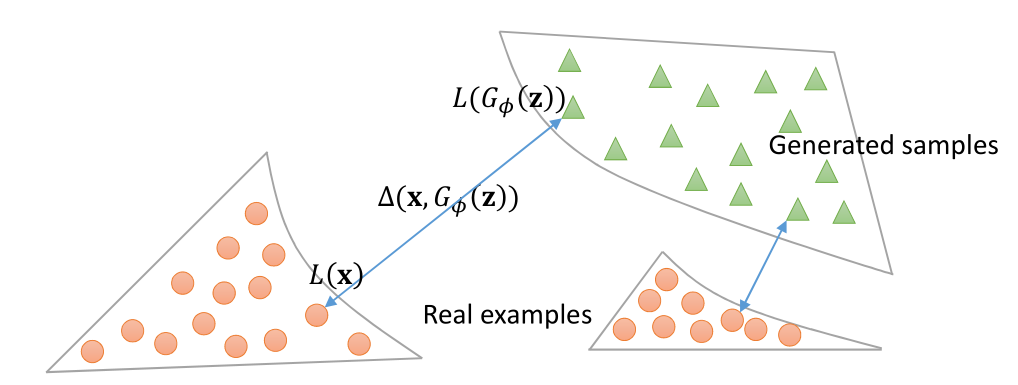
文章的一个重点就是强调将LS-GAN限定在Lipschitz密度上,同时限制住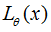 的建模能力到Lipschitz连续的函
数类上,从而实现了了LS-GAN得到的生成样本密度与真实密度的一致性,这一块我将在附录中简单证明一下。所谓的Lipschitz密度就是要求真实的密度分
布不能变化的太快,密度的变化随着样本的变化不能无限地大,要有个度,不过这个度可以非常非常地大,只要不是无限大就好。文章用了大量的笔墨在证明
LS-GAN在梯度消失上的优越性,但是推证的公式我不是很理解,但是通过作者的阐述知道:
的建模能力到Lipschitz连续的函
数类上,从而实现了了LS-GAN得到的生成样本密度与真实密度的一致性,这一块我将在附录中简单证明一下。所谓的Lipschitz密度就是要求真实的密度分
布不能变化的太快,密度的变化随着样本的变化不能无限地大,要有个度,不过这个度可以非常非常地大,只要不是无限大就好。文章用了大量的笔墨在证明
LS-GAN在梯度消失上的优越性,但是推证的公式我不是很理解,但是通过作者的阐述知道: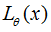 的上下界是分段线
性的,这种分段线性的函数几乎处处存在非消失的梯度,这样适当地控制
的上下界是分段线
性的,这种分段线性的函数几乎处处存在非消失的梯度,这样适当地控制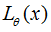 地学习过程,在这两个上下界之间最优
地学习过程,在这两个上下界之间最优
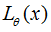 是不会出现饱和现象从而达到梯度不消失的情况。
是不会出现饱和现象从而达到梯度不消失的情况。
LS-GAN和GAN一样是一种无监督的学习算法,对于LS-GAN通过定义适当的损失函数,它可以非常容易的推广到有监督和半监督的学习模型。比如,我们可以
定义一个有条件的损失函数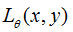 ,这个条件y可以是输入样本x的类别。当类别和样本一致的时候,这个损失函数
会比类别不一致的时候小,文章给的损失函数为公式3,加入了标签y。
,这个条件y可以是输入样本x的类别。当类别和样本一致的时候,这个损失函数
会比类别不一致的时候小,文章给的损失函数为公式3,加入了标签y。
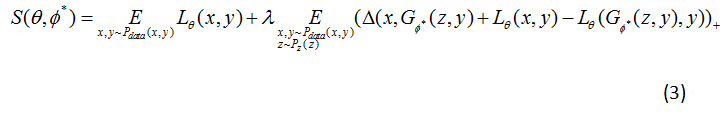
一旦得到损失函数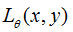 ,在给定一个样本x后,就可以用最小化损失函数的那个类别来对样本进行分类。
,在给定一个样本x后,就可以用最小化损失函数的那个类别来对样本进行分类。
小结:LS-GAN是在GAN的问题基础上展开的,对比WGAN各自拥有不同的优点。最终在GAN的基础上达到了按需分配的目的,让生成器和鉴别器生成的数据更 加的合理。下面是附录部分,大家可根据个人实际选择阅读。
附录

谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










