Adversarial Variational Bayes论文解读
VAE在数据编码得到的潜变量表示上很有启发性,可用于从训练数据中学习复杂的概率分布。Adversarial Variational Bayes 对抗变量贝叶斯(AVB)在VAE的基础上引入辅助判别网络(GAN)来实现用任意表达推理模型训练变分自动编码器,从而在VAE和GAN之间建立原则连接。 完善的数学理论依据加强了模型的可解释性,由于这篇论文涉及很多数学推证,如有理解错误请在评论区指出,谢谢!
论文引入
机器学习中的生成模型是可以在未标记的数据集上训练的模型,并且能够在训练完成后生成新的数据点。由于生成新内容需要很好地理解已有的训练数据, 因此这些模型通常被视为无监督学习的关键因素。近年来,生成模型变得越来越强大。虽然许多模型类如Pixel-RNNs,PixelCNNs,Glow展现了很好的效果, 但是两种最有名的要数变分自动编码器(VAE)和生成对抗网络(GAN)。
VAE和GAN都有各自的优点和缺点,虽然GAN在应用于学习自然图像的表示时通常会产生视觉上更清晰的结果,但VAE也很有吸引力,因为VAE可以自然地产生 生成模型和推理模型(隐空间)。将VAE和GAN结合的文章也是出了好多,VAE-GAN、CVAE-GAN、 BiGAN、AAEs。
VAE的最大缺点就是在生成上有些模糊,VAE不能产生清晰图像通常归因于在训练期间使用的推理模型通常不足以捕捉真实的后验分布这一事实。很多研究也证实了 使用更具表现力的模型类可以在视觉上和对数似然界限方面产生基本上更好的结果[1]。同样的,高度表达的 推理模型在强大的解码器的存在下是必不可少的,以允许模型完全利用潜在空间。
AVB就是尽量结合上述优点提出来的模型,这是一种训练变分自动编码器的技术,具有由神经网络参数化的任意灵活的推理模型。AVB也是将VAE和GAN结合, 在这中间AVB提出了严格的理论依据推导。总结一下,AVB具有的优点:
- 使用对抗性训练为变分自动编码器使用任意复杂的推理模型
- 对提出的方法给出了理论上的见解,表明在非参数极限中可以恢复真实的后验分布以及生成模型参数的真实最大似然分配
- 经验上证明模型能够学习丰富的后验分布
AVB模型
我们先来对比一下这篇论文提到的AVB和VAE的区别:
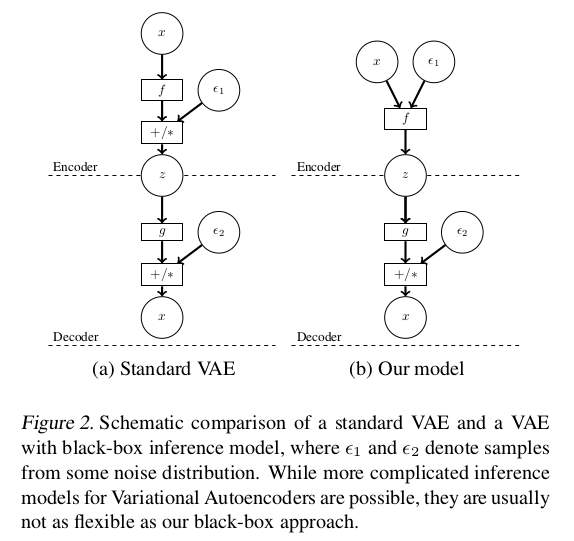
在结构上,AVB在Encoder上和VAE是不同的,标准的VAE在构造隐变量的时候,将隐变量分为均值和方差处理,并且通过符合$\mathcal N(0,1)$的噪声$\epsilon_1$ 来构造出隐变量$z$。而对应的AVB则是通过输入$x$和噪声$\epsilon_1$经过神经网络直接输出隐变量$z$。
对于标准的VAE,优化的损失函数为:
\[\begin{eqnarray} \max_{\theta} \max_{\phi} E_{p_{D(x)}}[-KL(q_{\phi}(z \vert x),p(z)) + E_{q_{\phi}(z \vert x)}log p_{\theta}(x \vert z)] \end{eqnarray}\]这里的$\theta$为编码器的参数,$\phi$为编码器的参数,$q_{\phi}(z \vert x)$为近似推理模型隐变量,$p_{\theta}(x \vert z)$为编码得到的生成数据变量, $p(z)$是先验分布,$p_{D(x)}$为真实输入数据分布。通常是标准正态分布。损失前半部分用于优化隐变量,后半部分优化重构出的数据,实现上, VAE是利用Encoder得到的均值和方差参与优化。
对于(1)式,可以写为:
\[\begin{eqnarray} \max_{\theta} \max_{\phi} E_{p_{D(x)}}E_{q_{\phi}(z \vert x)}[log p(z) - log q_{\phi}(z \vert x) + log p_{\theta}(x \vert z)] \end{eqnarray}\]公式(2)就是将(1)式中的KL一项展开以后,提取出$q_{\phi}(z \vert x)$就得到了(2)式。对于$q_{\phi}(z \vert x)$,如果有一个显示的表示, 比如$q_{\phi}(z \vert x)$神经网络参数化的高斯时可以使用随机梯度下降算法来优化,但是AVB中是利用黑盒子来表示$q_{\phi}(z \vert x)$, 所以还要做进一步变换。
AVB的思想就是引入GAN对抗思想,通过优化到判别网络$T(x,z)$的最优值来规避优化$log p(z) - log q_{\phi}(z \vert x)$的问题,具体的可以用公式 (3)来优化$T(x,z)$:
\[\begin{eqnarray} \max_T E_{p_{D(x)}}E_{q_{\phi}(z \vert x)} log \sigma(T(x,z)) + E_{p_{D(x)}}E_{p(z)} log(1 - \sigma(T(x,z))) \end{eqnarray}\]这里的$\sigma$可以理解为sigmoid函数,$T(x,z)$是为了区分采样对$(x,z)$是来自先验分布$p_{D(x)}p(z)$还是来自推理模型$p_{D(x)}q_{\phi}(z \vert x)$, 通过最大最小话博弈,最后实现平衡状态时,此时的推理模型$q_{\phi}(z \vert x)$可以很好的接近先验分布$p(z)$了。
判别网络最优化$T^*(x,z)$记为:
\[T^*(x,z) = log q_{\phi}(z \vert x) - log p(z)\]此时,公式(2)可以写为:
\[\begin{eqnarray} \max_{\theta ,\phi} E_{p_{D(x)}}E_{q_{\phi}(z \vert x)} (-T^*(x,z) + log p_{\theta}(x \vert z)) \end{eqnarray}\]公式(4)里的$T^*(x,z)$已经是优化过的最大值了。
总结一下,AVB在VAE的基础上引入了判别网络用于优化推理模型到先验分布,AVB有三大参数需要优化,分别为Encoder参数$\phi$,Decoder参数$\theta$ 和判别网络$T^*(x,z)$参数$\psi$,最后得到的算法框图为:

跟着思路捋一遍,AVB的模型还是比较清晰的,为了进一步提高模型,文章又做了自适应对比度改进。
自适应对比度
虽然在非参数极限中AVB产生了正确的结果,但实际上$T(x,z)$可能无法充分接近最优函数$T^*(x,z)$。该问题的原因是AVB计算两个密度$p_{D(x)}q_{\phi}(z \vert x)$ 与$p_{D(x)}p(z)$之间的对比度时这通常是非常不同的。然而,当比较两个非常相似的密度时,逻辑回归对于似然比估计最有效。为了提高估计的质量, 文章又引入辅助条件概率分布$r_{\alpha}(z \vert x)$具有近似$q_{\phi}(z \vert x)$的已知密度。例如,$r_{\alpha}(z \vert x)$可以是 具有对角协方差矩阵的高斯分布,其均值和方差与$q_{\phi}(z \vert x)$的均值和方差相匹配。利用这个辅助分布,我们可以重写变分下界公式(1)为:
\[\begin{eqnarray} E_{p_{D(x)}}[-KL(q_{\phi}(z \vert x),r_{\alpha}(z \vert x)) + E_{q_{\phi}(z \vert x)}(-log r_{\alpha}(z \vert x) + log p_{\theta}(x,z))] \end{eqnarray}\]同样的引入判别网络$T^*(x,z)$后,可以进步写为:
\[\begin{eqnarray} max_{\theta ,\phi} E_{p_{D(x)}}E_{q_{\phi}(z \vert x)} (-T^*(x,z) - log r_{\alpha}(z \vert x) + log p_{\theta}(x \vert z)) \end{eqnarray}\]$r_{\alpha}(z \vert x)$由于具有对角协方差矩阵的高斯分布给出的情况,其中均值$\mu (x)$和方差矢量$\sigma (x)$匹配$q_{\phi}(z \vert x)$的均值和方差。 由于KL散度在重新参数化下是不变的,因此(5)式中的第一项可以重写为:
\[E_{p_{D(x)}}KL(\hat{q}_{\phi}(\hat{z} \vert x),r_0(\hat{z}))\]其中$q_{\phi}(z \vert x)$表示归一化的分布$\hat{z} := \frac{z - \mu (x)}{\sigma (x)}$,$r_0(\hat{z})$为是高斯分布,均值为0,方差为1。 判别网络只需要考虑对于$q_{\phi}(z \vert x)$与高斯分布的偏差,可改善模型,伪代码如下:

AVB实验
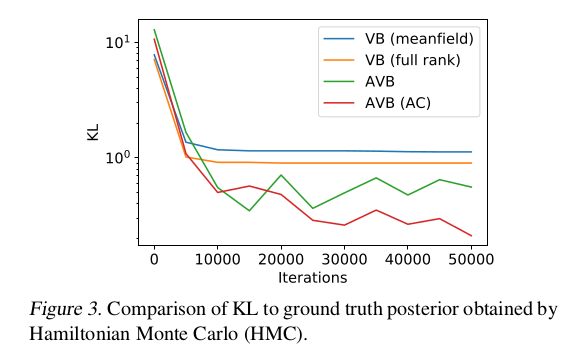
实验对比了AVB,VB和HMC是那种模型在STAN中实施的高斯推理模型[2]进行了比较,在KL距离上,实验结果如下:
定性分析上,AVB也展示了较好的生成结果:
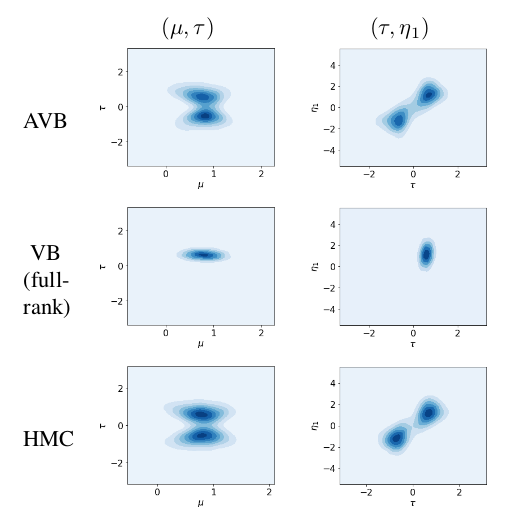
在潜在分布上,AVB相对于VAE将数据分布之间分的更加明显,同时也在最大似然上取得了优势:
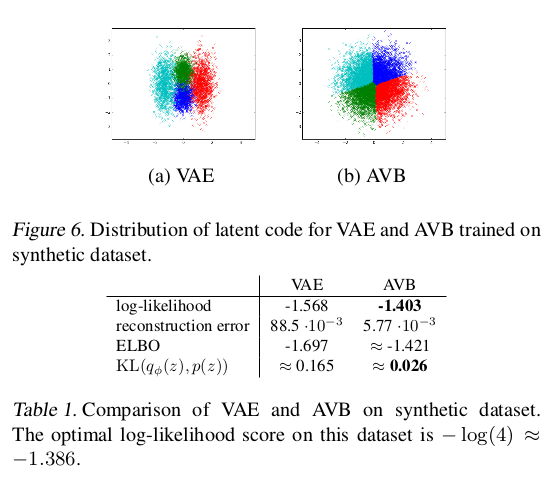
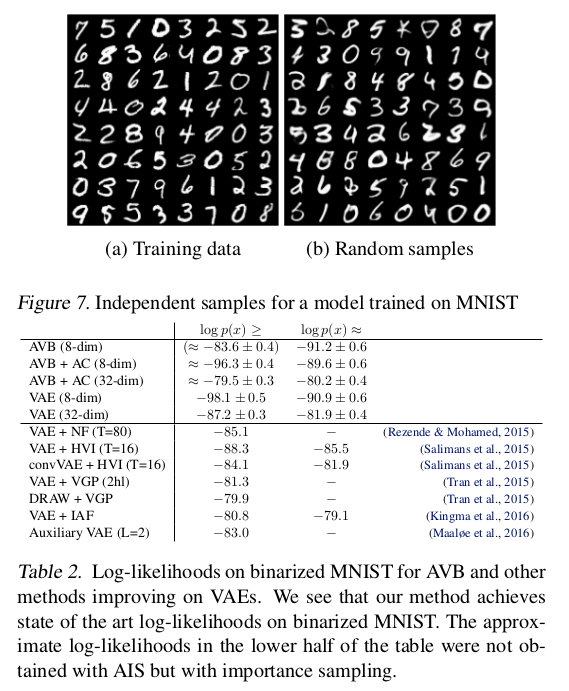
在随机生成上,文章在mnist上做了测试,在定量上也做了对比分析:
总结
文章基于对抗性训练为变分自编码器提出了一个新的训练程序。整体结构能够使推理模型更加灵活,有效地允许它代表潜在变量的几乎任何条件分布族。 通过对抗的引入,在潜在变量空间上学习上取得一定的进展,严格的理论已经也加强了方法的理论依据。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










