蒙特卡洛采样之拒绝采样(Reject Sampling)
我们所说的抽样,其实是指从一个概率分布中生成观察值(observations)的方法。而这个分布通常是由其概率密度函数(PDF)来表示的。而且, 即使在已知PDF的情况下,让计算机自动生成观测值也不是一件容易的事情。从本质上来说,计算机只能实现对均匀分布(Uniform distribution)的采样。 那如何实现计算机很好的采样数据样本呢?今天我们一起来看看实现方法。
在采样问题上我们可能会面对这些问题:
- 计算机只能实现对均匀分布的采样,但我们仍然可以在此基础上对更为复杂的分布进行采样,那具体该如何操作呢?
- 随机分布的某些数字特征可能需要通过积分的形式来求解,但是某些积分可能没有(或者很难求得)解析解,彼时我们该如何处理呢?
- 在贝叶斯推断中,后验概率的分布是正⽐于先验和似然函数之积的,但是先验和似然函数的乘积形式可能相对复杂,我们又该如何对这种形式复杂的分布进行采样呢?
针对这些问题衍生出一系列求解的方法。
Inverse CDF 方法
这种方法称为逆变换采样(Inverse transform sampling)法,我们一起来回顾一下PDF和CDF。
对于随机变量 \(X\),如下定义的函数 \(F\):
\[F(x)=P\{X\leq x\}, \quad -\infty <x<\infty\]上式称为\(X\)的累积分布函数(CDF,Cumulative Distribution Function)。
对于连续型随机变量\(X\)的累积分布函数\(F(x)\),如果存在一个定义在实数轴上的非负函数\(f(x)\),使得对于任意实数\(x\),有下式成立:
\[F(x)=\int_{-\infty}^{\infty}f(t)dt\]则称\(f(x)\)为\(X\)的概率密度函数(PDF,Probability Density Function)。显然,当概率密度函数存在的时候,累积分布函数是概率密度函数的积分。
所以,通常我们可以通过对PDF(如下图中的左图所示为正态分布的PDF)进行积分来得到概率分布的CDF(如下图中的右图所示为正态分布的CDF)。
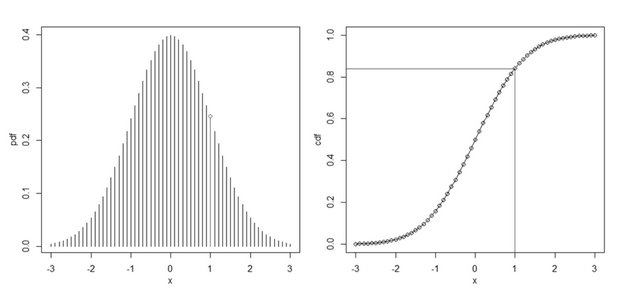
我们可以求得CDF的反函数\(F^{-1}(u)\),如果要得到 m 个观察值,则重复下面的步骤 m 次:
- 从 Uniform(0,1) 中随机生成一个值(前面已经说过,计算机可以实现从均匀分布中采样),用\(u\)表示。
- 计算\(F^{-1}(u)\)的值\(x\),则\(x\)就是从\(f(x)\)中得出的一个采样点。
在上图中,如果从 Uniform(0,1) 中随机生成的值\(u=0.8413\),则可以算得\(F^{-1}(u)=1\),则此次从正态分布中生成的随机数就是 1。
为了进一步验证Inverse CDF 方法真的有效,我们从定量上算一下。
假设现在我们希望从下面这个PDF中抽样:
\[f(x)=\begin{cases} 8x&, if\ 0\leq x<0.25\\ \displaystyle \frac{8}{3}-\frac{8}{3}x&, if\ 0.25\leq x\leq 1\\ 0&,otherwise \end{cases}\]可以算得相应的CDF为:
\[F(x)=\begin{cases} 0&, if\ x<0 \\ 4x^2&, if\ 0\leq x<0.25\\ \displaystyle \frac{8}{3}x-\frac{4}{3}x^2-\frac{1}{3}&, if\ 0.25\leq x \leq 1\\ 1&, if\ x>1 \end{cases}\]对于\(u\in [0,1]\),它的反函数为 :
\[F^{-1}(u)=\begin{cases} \displaystyle \frac{\sqrt{u}}{2}&, if \ 0 \leq u<0.25\\ \displaystyle{1-\frac{\sqrt{3(1-u)}}{2}}&, if 0.25\leq u \leq 1 \end{cases}\]通过计算求解(python程序近期上传),我们可以拟合出真实曲线和采样绘制出的曲线:
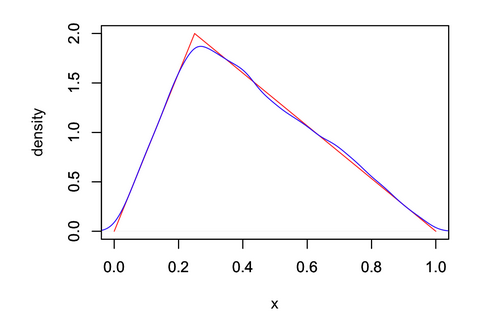
从图中可以看出,采样点与原始分布非常吻合。
拒绝采样(Reject Sampling)
从上述描述中可以知道Inverse CDF 方法确实有效。但其实它的缺点也是很明显的,那就是有些分布的 CDF 可能很难通过对 PDF 的积分得到, 再或者 CDF 的反函数也很不容易求。这时我们可能需要用到另外一种采样方法,这就是我们即将要介绍的拒绝采样。
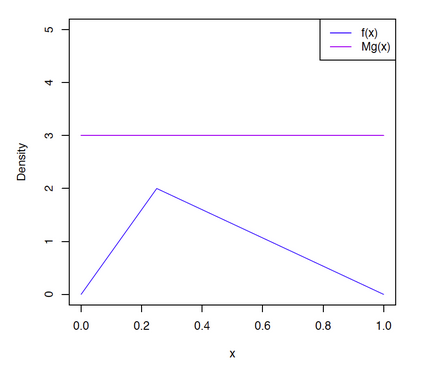
下图解释了拒绝采样的基本思想,假设我们想对 PDF 为\(p(x)\)的函数进行采样,但是由于种种原因(例如这个函数很复杂),对其进行采样是相对困难的。 但是另外一个 PDF 为\(q(x)\)的函数则相对容易采样,例如采用 Inverse CDF 方法可以很容易对对它进行采样,甚至\(q(x)\)就是一个均匀分布 (别忘了计算机可以直接进行采样的分布就只有均匀分布)。那么,当我们将\(q(x)\)与一个常数\(M\)相乘之后,可以实现下图所示之关系,即 \(M\cdot q(x)\)将\(p(x)\)完全“罩住”。

然后重复如下步骤,直到获得\(m\)个被接受的采样点:
- 从\(q(x)\)中获得一个随机采样点\(x(i)\)
- 对于\(x_i\)计算接受概率(acceptance probability) \(\displaystyle \alpha = \frac{p(x_i)}{Mq(x_i)}\)
- 从 Uniform(0,1) 中随机生成一个值,用\(u\)表示
- 如果\(\alpha \geq u\),则接受\(x_i\)作为一个来自\(p(x)\)的采样值,否则就拒绝\(x_i\)并回到第一步
当然可以采用严密的数学推导来证明Reject Sampling的可行性。但它的原理从直观上来解释也是相当容易理解的。你可以想象一下在上图的例子中, 从哪些位置抽出的点会比较容易被接受。显然,红色曲线和绿色曲线所示之函数更加接近的地方接受概率较高,也即是更容易被接受,所以在这样的地方采到的点就会比较多, 而在接受概率较低(即两个函数差距较大)的地方采到的点就会比较少,这也就保证了这个方法的有效性。
为了验证,我们还是以本文最开始给出的那个分段函数\(f(x)\)为例来演示 Reject Sampling 方法。如下面图所示,参考分布我们选择的是均匀分布 (你当然可以选择其他的分布,但采用均匀分布显然是此处最简单的处理方式)。而且令常数\(M=3\)。
得到的结果如下:
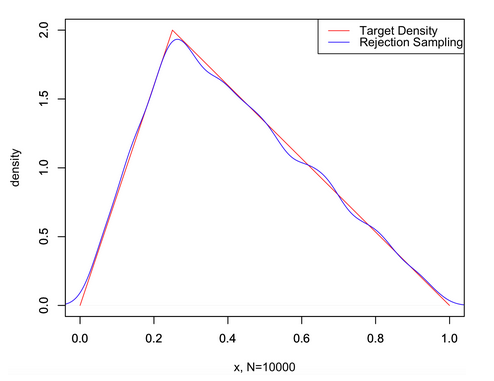
从实验结果来看,采样还是很可观的。
总结
拒绝采样对于概率分布函数难以求解的数据进行采样是有效的,现在计算机的计算能力如此发达的情况下,更是有利于蒙特卡罗采样的发展。
谢谢观看,希望对您有所帮助,欢迎指正错误,欢迎一起讨论!!!










